Early Warning and Early Response, by Susanne Schmeidl and Howard Adelman (eds.)

 

10. An Early Warning about Political Forecasting:
Oracle to Academics

Dipak K. Gupta
Fred J. Hansen Professor of Peace Studies
San Diego State University

Abstract

While we develop quantitative models for forecasting political and humanitarian crises, questions linger about their efficacy. In econometrics, there are accepted methodologies for determining the closeness of fit between the predicted and observed values. However, apart from the challenges of appropriate data and methods of analysis, many of these standard techniques either a) tell us little about the relative efficiency of our forecasting model or b) they do not even apply to the prescriptive models. This is because, first, after decades of economic forecasting, empirical evidence suggest that no single method predominates over others. Second, since EW models are for directing public policy, the predicted values are not independent of the observed values. That is, if a model places a nation on its list of highest risk, which provokes the intended policies for averting the crisis and the early actions are successful, then how do we measure the model’s success? In this paper, I emphasize that these models should not be considered as “forecasts” and should be taken as “warnings.” Therefore, we should acknowledge that the EW models offer one of the best tools for managing future humanitarian and political crises, but at once recognize their shortcomings.

“Is ‘Bosnia’ the last dark page of the 20th century or the first page for the next? The truth, I think, is that the world of tomorrow resembles Bosnia.... Bosnia serves as the a warning. We need mechanism to stop Bosnias in the future.”

— Haris Silajdzic Bosnian Prime Minister 1

 

Two golden rules of forecasting: It is extremely difficult to forecast, especially the future. But, if forecast you must, forecast and forecast often.

 

I. Introduction ₂

In 1992, The UN Secretary General called attention of the international community to the security threats arising from ethnic, religious, social, cultural or linguistic strife. In his Agenda for Peace, Boutros Boutros-Ghali emphasized the need for systematic efforts directed toward developing early warning systems. This new agenda paved the way for the UN Department of Humanitarian Affairs and the Centre for Documentation and Research of the UN High Commission for Refugees to carry out systematic research and data analysis for developing an early warning system (EW from now on). Today a number of prominent researchers in various universities, NGOs, and national and international governmental agencies all over the world are currently engaged in developing such a system for political crises, genocides and refugee migrations. Although efforts at building EW models are fairly new in the field of political and humanitarian crises, early warning models cover an wide range of phenomena from natural disasters, such as earthquake and flood, to outbreak of epidemics and famines.

From the earliest times of recorded history people have tried to forecast the future; they have attempted to develop early warnings for disasters to come by interpreting omens from animal entrails to tea leaves. In the book of Genesis, Joseph, after being betrayed by his brothers, languishing in prison, used his skills to gain the Pharaoh’s favor by successfully interpreting his dreams. One night, the Pharaoh had a dream; seven fat cows were grazing happily while seven lean cows emerged from the ocean and proceeded to devour the fat ones. Confused, the Pharaoh sought an explanation. No one in his kingdom could offer a satisfactory explanation. However, Joseph interpreted the dream right. He warned the Pharaoh that there would be seven years of bountiful harvest followed by seven years of drought. So, he advised the Pharaoh to stock up his granaries during the fat years to prepare for the leaner ones. His early warning was proven right, and while Canaan and the surrounding areas were suffering, Egypt was able to avert the ravages of a disastrous drought. Throughout history people have feared the unknown future and have attempted to bring it within the realm of systematic analysis; frightened individuals as well as the political leaders of all ages have sought early warning of impending doom from the shamans, oracles, astrologers, holy men, and lately, the academics.

Within social sciences, forecasting has largely been the domain of the economists. Emboldened by the policy implications of John Maynard Keynes’ empirically testable hypotheses, economic profession went full steam into the business of forecasting. Today we see established corporations such as the Data Resources, Inc., Chase Econometrics, as well as many government agencies including the Office of Management and Budget and Congressional Budget Office routinely engage in economic forecasting. Modern economies all over the world are heavily dependent upon forecasting of their economic stabilization policies. By using large econometric models, the effects of a tax increase or decrease are analyzed; monetary policies are guided by early warnings of leading economic indicators. Although economic forecasts like the weather report are often objects of much derision, evidence based upon long term data is fairly clear; we have been able to avert the extreme swings of business cycles in the post war year compared to those previous to the Wars. The virtual explosion in ethnic violence in the late 1980s and early 1990s, coupled with decades long quantitative research into the causes of collective violence have generated enthusiasm for forecasting of political and humanitarian crises.

The Hazards of Political Forecasting

Forecasting, especially of catastrophic events, however, carries its own hazards. For instance, forecasts of cyclones, epidemics and earthquakes can impose tremendous economic and political costs to the affected regions. Therefore, responsible forecasters must always be concerned about making false positive (predicting a crisis when nothing happened in reality) or false negative (predicting calm, yet the nation experiences an upheaval) predictions. ₃

In the mean time, a number of scholars have expressed deep skepticism regarding our ability to forecast political events. ₄ For instance, the failure of the intelligence community and political pundits to predict the sudden demise of communism in the Soviet Union and other parts of Eastern Europe, Timur Kuran has argued about our inability to forecast the future, when it comes to war and revolution. ₅ Kuran bases his analysis on peoples’ practice of falsifying their private preferences fearing government oppression, reprisal by other powerful forces in the society or peer pressure. If nobody expresses his or her true preference, the observers have no knowledge about the extent of antipathy toward the established political system. However, when a small crack appears in the seemingly solid edifice, people join the bandwagon in increasing rate finding comfort in the anonymity of large number of protesters.

For instance, consider a country where there is long simmering discontent among its populace. However, since not enough people are publicly articulating their opposition to the established regime, there is an outward calm. Now if there is an incident (which may appear to be relatively insignificant in the larger perspective) that causes active opposition from a small group of people, it may start a chain reaction, which may breakdown the inertia of a rapidly growing segment of the society. ₆ Just like a hand clap may bring about a huge avalanche, a small shift in public preference can set in motion a momentous change in the political landscape of a nation. Kuran has demonstrated with numerical examples various possibilities where a small event may cause a large outcome or when a very large event fails to mobilize the population. For instance, consider a society of 10 people, where the potential participants are lined up as follows: ₇

Individuals	a	b	c	d	e	f	g	h	i	j
Thresholds	10	10	20	30	40	50	60	70	80	90

The threshold figures represent the individual members’ preference for exposing their private preferences (to oppose the government) when the expected opposition reaches a certain level. Thus, individuals a and b would like to join the forces of rebellion when at least 10 percent of the population has come out publicly dissenting with the authorities. Individuals c through j require progressively higher levels of expressed public opposition. In this case, suppose for some reason, a experiences some unpleasant encounter with the government which prompts him to take a public stance against the authorities (an example of an external shock). His action will create a situation where b will now be embolden to take part in the anti-establishment movement, since it will satisfy b’s required threshold level of 10 percent mobilization. When b joins the movement, with a 30% mobilization, c will find it safe to add his voice to collective dissent. As a result of a small change in the publicly held position of a, quickly, the entire population will join in, causing a massive uprising.

In contrast, consider the following threshold levels:

Individuals	a	b	c	d	e	f	g	h	i	j
Thresholds	0	10	20	40	40	50	60	70	80	90

In this case, individual d is much more circumspect and will not join unless at least 40% of the population have expressed their opposition to the regime. In that case, when a (an already disgruntled revolutionary, with threshold level of 0) starts the chain reaction, it stops with only 30% (a, b, and c) mobilization. Since the rest of the population does not change their public positions, even if there is a great deal of grievances, expressed opposition will remain confined within a relatively small minority.

Thus, keeping the complexity of social upheavals in mind, many scholars have expressed serious doubts about our ability to develop a successful early warning system of political and humanitarian crisis. Yet, forecasting is to planning as breathing is to living. If we want to respond quickly to the humanitarian catastrophes, we must plan in advance, we must recognize the problems before they become overwhelming, we must identify the nations and minorities at risk. Although efforts at forecasting political and humanitarian crises are still at their infancy, the possibility of disappointment with early warning results, prompted Professors Gurr and Harff to warn that “if early warnings are too often inaccurate, early warning research may be discredited.” ₈

The Problem

The purpose of this article is to address the questions:

• What are the most commonly used models of forecasting?
• What is the current state of political forecasting?
• How do we measure relative accuracy of the forecasts?
• How do we choose among the models?
• What have we learned about forecasts?
• How to improve forecasting accuracy?
• Finally, what can we expect from early warning forecasts?

Although forecasting and developing EW models are fairly routine in economics, it is relatively new in the realm of political science. Yet, econometric literature is not particularly rich in explaining how to evaluate a forecasting model, especially those used for policy analyses. Is accuracy in forecasting the only criterion for choosing a particular EW model or should we consider other factors as well. In this article, after reviewing the relevant literature, I would like to examine the question of evaluation of forecasting methods. In this context, I would also like to ask the question: “How much can we expect from the our forecasting exercises?” The purpose of this article is not to pick one method of forecasting over others, but to delve into the criteria for choosing the method of developing an early warning and to explore ways of making forecasts more accurate. We conclude that a model of early warning must be treated as an warning rather than as a forecast or prediction. In sum, echoing the sentiments of the former Secretary General of the United Nations, I argue that although it is impossible to forecast the exact outcome, the development of EW models remains one of the best chances of managing the devastating effects of wars within nations.

 

II. Types of Forecasting Models: A Quick Tour

The myriad forecasting techniques may be classified in two broad (and often overlapping) categories. We may call the first Data-based and the second, judgment-based methods of forecasting. The data-based forecasting requires the collection of large data sets either over time and/or over cross-section of the cases, and the use of statistical analysis of the data. In contrast, for the expert-based methods, the preponderant emphasis is not on the collection of data or its systematic analysis but on the subjective assessment by the experts based on relatively less specified methodology. Figure 1 describes the taxonomy of the major forecasting tools.

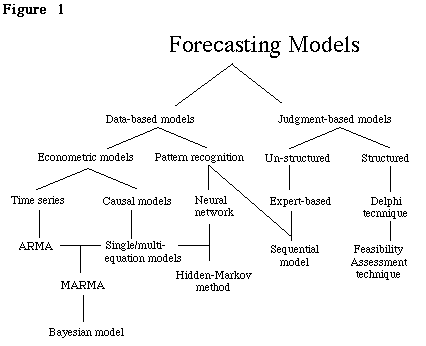
The category of data-based analysis can be further sub-divided into those based on standard econometric models and those which use new methods of pattern recognition. The econometric method of forecasting involves developing detailed statistical models. The econometric models can once again be divided into causal models and time-series models. Causal analysis requires the analyst to specify the causal linkages which bind the dependent variable with a set of independent variables. Thus, in causal analysis, the value of the dependent variable (Yt) at time (t) is explained with the help of a number of independent variables (Xit): Yi = + iXi +
where: and i are the estimated coefficients and e is the random error term.

The resulting model can then be estimated with the help of either a single equation Classical Least Square (CLS) method or by using a large set of simultaneous equations through multi-stage estimation techniques. Many governmental agencies and for-profit forecasting outfits derive their forecasts by running simultaneous equation models with large number of interdependent equations.

However, of late, econometricians are increasingly using time-series analysis for forecasting economic trends. ₉ In time-series analyses, we do not look for causal linkages; there is no effort made to explain the “why” of events. Instead, they rely on the hypothesis that every data series, spanning a long enough time period consists of an underlying pattern + randomness effects of variables extraneous to the model. The object of time-series analysis is to describe the pattern and minimize the domain of random effects. The trend pattern of a time-series model can be evident when the series is smoothed through moving average. In the moving average method, the forecasts for the period (t+1) is given by averaging the data of the past periods. However, as the series progresses over time, our moving average forecasts are often not accurate due the effects of random variations. This random variations can be minimized by adjusting the target by the amount of the past period’s mistake. This is the process of auto regression. By combing auto regression (AR) with moving average (MA), the method of ARMA is created.

However, the random effects can include the impacts of natural disasters, a sudden change in preference pattern, or a sudden shift in government policy. Therefore, some effort have gone into developing a hybrid model by combining causal analysis with ARMA model. This is called multivariate ARMA or MARMA. ₁₀

There is yet another approach to forecasting of a series is a variation of MARMA. Where we engage in serial forecasts, we can learn from our past mistakes in forecasting. The Bayesian forecasting or Kalman filter is designed to take advantage of the latest actual value of the dependent variable as well as its corresponding forecasts. Based on the two information, forecast for the future value of Y is specified as:

Ft+1 = Yt + (1- ) Ft

where, is the relative weight that we attribute to the current period’s (t) actual and forecasted values. The Baysian forecasting method attempts to estimate the optimal value of . If there is less uncertainty about the future, then we attribute a lower weight to our forecasted value of the current period. In the extreme case of certainty where the future is perfectly predicted by the current period, will be equal to 1. Clearly, then, as uncertainty goes up, we place more weight on the forecasted value, which is estimated from information of the entire past series. ₁₁ In the extreme case, where the immediate past is no indicator of the past, is set equal to 0. The most important assumption about Bayesian forecasting is that the actual and the forecasted values are independent of each other.

It should be intuitively clear that time series analyses work best where there is a more or less monotonic (without bending backward) trend. Thus, most national economic and demographic data series exhibit upward trend with fluctuations due to the effects of business cycles, seasonality or impacts of some other random (or unaccounted for variable in the model) variable. However, decades of extensive uses of the various kinds of models have yielded some counter-intuitive results about the relative efficacy of the two types of econometric modeling.

The other branch of data-based models is what we may call, pattern recognition. These techniques do not necessarily want to find the relative strengths of the causal variables by linking them to the dependent variable. And, unlike the time-series models, they do not make the assumption of a trend pattern linking the dependent variable to its previous values. In stead these models attempt to locate the variables which were present the previous times an event had taken place. Based on that information, this set of techniques attempt to find the presence of similar variables in the current condition to forecast the future. Pattern recognition can be done by neural networking, where based on the past occurrence of events, the computer model is “trained” to recognize the essential pattern. However, the broad category of pattern recognition offers two hybrid kinds of methods. The Hidden Markov method uses the neural network model to estimate the elements of the transitional matrix (Reference to HMM). Another hybrid variation of the pattern recognition technique is where the essential patterns of the dependent variables are a) recognized from past experiences; b) extensive data on these variables are collected and c) based the presence of these variables, expert-based predictions are made. Harff (in Gurr and Harff, 1996) called this the Sequential Model of forecasting.

Many of the judgmental or subjective methods of forecasting techniques were created during the World War II as a means of military strategic planning. In due course, these systematic analyses of expert opinion have found its place in the forecasting literature. However, most textbooks on forecasting place them at the end of the book, almost as afterthought. Yet, owing to a number of shortcomings of the objective methods as well as new advancement in cognitive sciences, the expert-based forecasting methods are increasingly finding their place in the sun. The judgmental models can be divided in two major groups: those which use structured methods of arriving at expert forecasts and those which do not. For instance, the Delphi method of forecasting would go through a definite set of rules to keep the panel of experts free of “group-think” by systematically polling the experts anonymously and distributing the statistical compilations of the responses for successive iteration of the process (Dunn, 1994).

In contrast, unstructured method of forecasting follow no such definite procedural steps. In an unstructured model, an expert or even a group of experts can draw conclusions about the future course based on their accumulated knowledge. For instance, most of the public sector planning is conducted on the basis of forecasted values of future revenues, needs etc. Frequently, such decisions are made by a group of experts agreeing to a “reasonable” rate of growth. ₁₂

 

II. Political Forecasting: A Brief Review

In political science, the entry of forecasting is relatively new and until recently, has been confined mostly in the area of election outcomes through opinion polling. Political scientists have come a long way since 1936 when, based on a their subscription list and a random telephone survey, Literary Digest boldly predicted electoral victory for Alf Landon and a sound defeat of President Roosevelt by nearly 3 to 1 margin. ₁₃ However, when the actual results were out, it was Roosevelt who won the election by a landslide. Since then, the doomed magazine has defined a textbook case of a biased samples; in 1936 telephone was but an instrument of selective ownership and the subscription list of the literary journal certainly did not represent the cross-section of the population. Today, in the United States, unless the voters have reasons to hide their true preferences and deliberately falsify responses, ₁₄ the forecasts of electoral fortunes have been quite accurate.

This is not to say that there has been a dearth of sophisticated quantitative analyses in political science. Over the last three decades much scholarly effort has gone toward building econometric models, virtually in all branches of political science, especially in the areas of comparative politics. However, a few, if any, until quite recently, have considered using their models for forecasting. Although EW models for political and humanitarian crisis is still at its infancy, a significant number of scholars from many parts of the world are attempting to develop such models. ₁₅

Econometric models

Inspired by the introduction of empirically testable hypotheses by Professor Gurr (1970), the area of comparative politics that has enjoyed a long history of empirical model building is the analysis of cross-national political rebellion. ₁₆ Almost all of these comparative studies used causal analysis on cross-national data. However a few others have used time series or ARMA models. ₁₇ Even though these models were based on econometric modeling, their primary purpose was analytical; with the exception of Gurr and Lichbach (1986), most these researchers made no attempt to forecast the future values of their dependent variables. ₁₈

In his more recent work, Professor Gurr (1993) broke tradition with the previous studies by gathering comparative data on sub-national minority groups. On the basis of this information, Gurr and his associates proceeded to forecast risks facing minority population groups around the world. Gurr bases his forecasting on the basis of three broad categories of variables: regime durability, resource base, and regime democracy. He argues that durable nations, with their long-standing tradition of governance will be less amenable to engage in gross violation of human rights. Similarly, if nation has deep resource base, it can easily co-opt the opposition without having to coerce with extreme force. Finally, data suggest that democracies are less likely to resort to violent repression than their authoritarian counterpart. Based on these three variables, Gurr analyzed the relative proneness of a particular society being involved with genocide and gross violation of human rights of a minority group within its political boundaries.

In continuation of his work, Gurr and Moore (1996) combined Gurr’s hypothesis of relative deprivation (group grievances) with Tilly’s (1978) mobilization as explanations of states’ repressive behavior toward minorities within its political borders. Based on a three-stage least square method, Gurr and Moore analyzed minority group rebellion as a result of interaction with repression, grievances and mobilization. Based upon their estimated results, Gurr and Moore developed their early warning forecasts for the 1990s.

Similarly, in the area of refugee migration, Jenkins and Schmeidl have attempted to develop causal models based on multiple regression models (see Jenkins and Schmeidl, 1996; and Schmeidl and Jenkins, 1996). Their results point to the fact that ethnic discrimination gives rise to large scale refugee migration, especially when the state becomes weak. Further, mass trans-national movements of people are also likely when there are non-violent protest demonstrations in authoritarian regimes.

Models of Pattern Recognition

The models of pattern recognition require the collection of large amounts of data but they do not attempt to estimate the coefficients, measuring the strength of their association with the dependent variable. In this area, Peter Brecke (1997) has been experimenting with neural networking models. The problem of EW is that it is often not “early” enough (see Schmeidl and Jenkins, 1997). The policy makers may require quick or even real time analyses of events data, which elaborate econometric models are often unable to do. The advent in computer technology and information gathering, transmitting and processing have allowed a number of researchers to look into new ways of developing EW signals. A number of different data systems have sprung up in developing real time early warning system. For instance, the Global Events Data System (GEDS) is capable of generating conflict indicators on a near real time basis (Davies and McDaniel, 1996).

However, their coding is done by hand and, therefore, the results are not instantaneous. The drive to develop even faster warning have prompted researchers to seek help from the recent advancements in artificial intelligence and develop computer-based coding. These systems are able to glean the essential information automatically from electronic transmissions of a wide-ranging texts, such as news reports from the wire services, diplomatic cables, and electronic mail messages sent by the NGO field observers. Thus, the Kansas Events Data System (KEDS) codes interactions among the parties in the Middle East by using Reuters World Newswire (Schrodt, 1995, 1997; Gerner et al. 1994). Similarly, the Protocol on Nonviolent Direct Action (PANDA) rely on sparse parsing techniques to code a wide-ranging events data on political conflict on a world-wide basis (see, Bond and Bond, 1995; Bond et al. 1996). In further refinement of the technique, Bond (1997) has recently created an integrated system, Find-Read-Extract-Display (FRED), which is able to link microcomputer spreadsheets and produce graphics on a real time basis.

The recognition of pattern may not be sanitized by automatic coding and “training” of the computer to recognize the pattern for the forecast of political and humanitarian disasters. In a hybrid effort, pattern recognition may be mixed with expert opinion or the use of political theory. Another group of studies, without employing any strict methodology of analytical techniques, have broadened our horizon of knowledge in the areas of monitoring and forecasting of genocides and politicides. Posing the question, “Can we predict genocide?” Harff proceeds to develop what she calls sequential modeling. ₁₉ I should point out here that I do not use the term “unstructured” to mean seat-of-the-pants analysis. These, like the one proposed by Harff are grounded in theories of human motivations. However, for these models, theory goes up to the selection of the relevant variables and their measures. Once the data is assembled, there is no defined structure; much like the economic forecasts based on the leading economic indicators, forecasts are done by experts by reviewing the development in the political/military environment.

For instance building upon her past theoretical work on politicide and genocide (1987; 1992), Professor Harff (1996) advocates the “sequential model.” This model includes national and international background conditions, intervening conditions, and the “accelerators.” Harff defines accelerators as “events outside the parameters of the model: they are essentially feedback events that rapidly increase the level or significance of the most volatile of the general conditions, but may also signify system breakdown or basic changes in political causality.” After the relevant data is called from the news reports and other reliable sources, these factors are coded. Based on this information, early warning forecasts are made.

Structured Judgmental Methods

Although it is not clear whether good data precedes good theory, quantitative analysis mushrooms when systematic data are kept. In fact, the earliest empirical analyses were based on national demographic data, thereby acquiring the name “statistics” (numbers relating to the state). In a similar fashion, when keeping of systematic data on conflict between nations were started, an impressive number of books and articles developed analytical models for analyzing and eventually forecasting war between two nations. ₂₀ Most of these models benefited from systematic analysis of decision making under uncertain conditions. Most of these efforts employ game theory and expected utility models for forecasting of international hostility. This group of studies starts with four sets of explicit or implicit assumptions about the process through which two rival nations engage each other in warfare: ₂₁

• Competition between groups produces political conflicts
• Groups compete over specific policy-related issues
• A strong leader dominates each group
• Each strong leader is a rational decision maker who seeks to maximize expected utility.

Bueno de Mesquita et al. (1985b) developed the analytical scheme shown in Figure 2. As can be seen from the diagram, the expected payoff of the government has been mapped on the horizontal axis, while the vertical axis maps the expected payoff of the opposition. The individual quadrants on the diagram have been marked with heavy Roman numerals. In the top right hand quadrant both the parties expect to gain from a confrontation. Therefore, we can expect that in such a situation the risk of confrontation remains high. In segment I, the government expects to gain more from a confrontation than does the opposition, therefore, we can expect the government to initiate a policy of direct confrontation. Similarly, in II, it the opposition which can expected to lead the confrontation. In the upper heft-hand quadrant, the opposition expects to gain from a confrontation while the government expects to lose. Therefore, one can expect a compromise. However, in segment III, the government’s loss is less than the opposition’s win. Hence, in such a situation, there will be a negotiated settlement where the government is likely to give up some to avert a direct confrontation. In the IVth segment, the government loses a lot more than the opposition gains from an open hostility. This is likely to bring about a government initiated peace settlement. The Segments VII and VIII are the mirror opposite of III and IV. Finally, when reality reflects a situation close to the lower left hand quadrant, where both parties expect to lose from confronting each other, we can safely expect a stalemate with little or no confrontation. Bueno de Mesquita and his associates attempt to gauge the “expectations” of the parties by combining expert opinion with the structure of FAT.

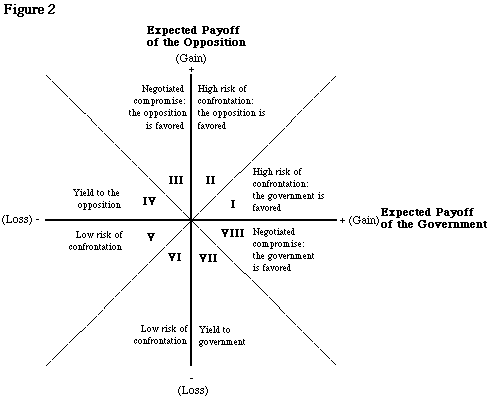
Thus, Bruce Bueno de Mesquita analyzes expert-based judgmental method of forecasting similar to Feasibility Assessment Technique. ₂₂ In his scheme, systematic data is presented to a small group of country experts who determine the relative positions of the most influential players in the game on a ratio scale between +1 and -1. Similarly, the relative assessment of available resources of the players along with their levels of commitment are made by the experts on a scale between 0 and 1. By multiplying the three values and adding them up for all the players (relative value position x available resources x commitment) the future outcomes are estimated. ₂₃ Based on these two models, Bueno de Mesquita and his associates have forecasted a wide variety of political events, including the political future of Hong Kong after the Chinese takeover (1985b) and the political developments in the post-Khomeini Iran (1984)

 

IV. Measuring Relative Accuracy of the Forecasts: How Good Are They?

Scholars who have examined the relative effectiveness of predictive theories from epistemological standpoint, have put the question of relative efficiency under analytical microscope. However, wherever they start from, the examiners end up looking at the forecasting models linking the forecasted values to the actual observations. So important is this congruence that Milton Friedman in his seminal article (1953) asserted that a theory should be judged not for its assumptions (as economists are frequently questioned on their unrealistic assumptions about human behavior) but for its predictive abilities. Some scholars have expanded this simple criterion for the choice among theories, but their emphasis remains similar in spirit. For instance, philosopher of science Imre Lakatos (1978) suggests that :

A scientific theory T is falsified if and only if another theory T’ has been proposed with the following characteristics: (1) T’ has excess empirical content over T: that is, it predicts novel facts, that is, facts improbable in the light of, or even forbidden, by T’; (2) T’ explains the previous success of T, that is all the unrefuted content of T is included (within limits of observational error) in the content of T’; and (3) some of the excess content of T’ is corroborated.

In other words, we should choose theory (or a predictive model) T’ over T, if T’ is able to explain more than what T could, and its excess predictability can be empirically verified. However, while the epistemologists are certain about the need for predictive accuracy, there is hardly a unanimity within the ranks of the econometricians about how to measure forecasting accuracy.

Measuring Forecasting Accuracy

The question of measuring forecasting accuracy is particularly difficult one. ₂₄ However, before proceeding with the question, we should note that forecasts are often made in terms of probability. Few would want to predict uncertain future events with categorical certainty. When it comes to stochastic forecasting, performances can be improved through calibration, discrimination, and correlation.

Calibration:

Let us assume that over the last decade, we have observed and had predicted outcomes of political crises in 100 cases. Table 1 resents the hypothetical data In case, we are assuming that we have identified five stages of political crisis, measured by the number deaths. ₂₅ Let us suppose, we have defined five different stages of political and humanitarian crisis, measured in terms of the number of deaths due to political protest or government reprisal. We have defined the five stages as follows:

Massive uprising	over 100 deaths
Serious uprising	between 99 and 50 deaths
Moderate uprising	between 49 and 10 deaths
Low-Level protests	between 9 and 1 deaths, and
Calm	no reported deaths

In Table 1, the first column explains the categories of political and humanitarian crisis, the second column shows the actual number of deaths while the remaining columns record the previous predictions, which were made before the events actually took place.

Table 1: Chart of Hypothetical Prediction

Categories of political crisis (number of deaths)	Total number of actual incidents	Prediction of Massive uprising > 100 deaths	Prediction of Serious uprising 50–99 deaths	Prediction of Moderate uprising 10–49 deaths	Prediction of Low-level protests 1–9 deaths	Prediction of Calm 0 death
Actual occurrence of Massive uprising > 100 deaths	7	4	2	1	0	0
Actual occurrence of Serious uprising 50–99 deaths	10	1	5	2	1	1
Actual occurrence of Moderate uprising 10–49 deaths	13	1	2	8	1	1
Actual occurrence of Low-level protests 1–9 deaths	30	0	3	4	10	13
Actual prevalence of Calm 0 death	40	0	1	2	16	21
	100	6	13	17	28	36

We can read this Table by following the second and third columns: There were 7 incidents of massive uprising. However, we had forecasted such events 6 times, of which, 4 times our prediction coincided with an actual event, twice we observed a serious upheaval, and once each, there were moderate and low level disturbances. We did not observe any case where we had predicted a massive uprising and absolutely nothing happened.

Table 2: Probability Distribution of Actual and Predicted Events

Categories of crisis (number of deaths)	Frequency of actual events	Frequency of predicted values	Probability of actual events	Probability of predicted events
Massive > 100	7	6	.07	06
Serious 50–99	10	13	.10	.13
Moderate 10–49	13	17	.13	.17
Low-level 1–9	30	28	.30	.28
Calm 0	40	36	.40	.36
	100	100	1.00	1.00

A prediction is well calibrated when conditional expected outcomes, given the forecasts, are equal to the probability statement of the forecast.

Thus, our forecast will be considered well calibrated if, on the average, the probability of forecasts matches that of the actual outcome. ₂₆ For instance, we can see that the probability of a forecast of a massive event is 6% (out of 100 events, we had predicted 6 will be “massive”). Since this matches closely with the actual frequency of events (7%), we may consider our forecast to be good. In the case of perfect forecast, the probability distribution of the predicted values will exactly match that of the actual event. Figure 3 shows the calibration plot of our hypothetical humanitarian disaster forecast.

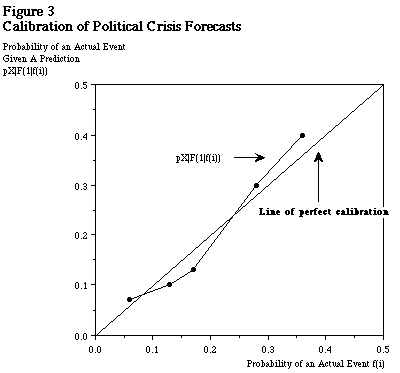
This simple, yet powerful plot demonstrates the difference between the relative frequency of occurrence and the probability of an actual event taking place given a certain forecast. ₂₇ In case of perfect forecast, the difference between the two becomes zero and the curve becomes a 45 degree line from the origin. From the diagram, we can identify those incidents for which we are over forecasting or under-forecasting. ₂₈

Discrimination:

Unfortunately, even the best calibrated model can yield worthless predictions. For instance, in the above example, we may duplicate the actual probability by simply filling up an urn with 100 balls, 7 of which, say is red, 10 blue, 13 black, 30 purple, and 40 white. Now, whenever we need to make a forecast, we draw a ball at random, replacing it immediately for the following draw. Clearly, in this case, the probability distribution of our predictions will match exactly that of the actual events, but the forecasts will be largely meaningless.

Therefore, along with calibration, we need to know discrimination of the forecasts. Discrimination looks at the probability distribution within each category of forecast and asks how many of the positive predictions (“it will happen”) coincides with actual events taking place and how many of the negative prediction (“it will not happen”) are associated with the event not taking place? Thus, if we are predicting a binary event X with forecasts (F), then we have the following possibilities:

Pr{F=1|X=1} = f1	Correct identification of event (predicted an event and it took place)
Pr{F=1|X=0} = f0	False Positive or “false alarm” (predicted an event but it did not take place)
Pr{F=0|X=1} = (1-f1)	False Negative or failure to detect (did not predict an event but it took place)
Pr{F=0|X=0) = (1-f0)	Correct identification of non occurrence (did not predict an event and it did not take place)

A well discriminated forecast will minimize false positives and false negatives. The concept of discrimination may be explained better by slightly changing the above example. Let us separate the data into two categories, incidents of deaths from political causes and no incident (calm). We can present the data as follows:

Table 3: Probability Distribution of a Binary Event

	Incidents	No incidents
Categories of crisis	Number of incidents with death predicted	Number of incidents with death not predicted	Relative frequency of successful prediction	Relative frequency of unsuccessful prediction	Cumulative probability of successful prediction	Cumulative probability of unsuccessful prediction
Massive > 100	7	0	.11	0	.11	0
Serious 50–99	9	1	.14	.03	.25	.03
Moderate 10–49	12	1	.19	.03	.44	.06
Low-level 1–9	17	13	.27	.36	.71	.42
Calm 0	19	21	.30	.58	1.0	1.0
Total	64	36	1.0	1.0

We may noted that I have calculated the relative frequencies for successful predictions for each category of violence by dividing the number of correct predictions by the total number of cases in that category. Thus, we can see that in the category of “massive” uprising, there were 7 incidents predicted. In all of those cases, there was loss of at least one life. Therefore, the relative frequency for successful prediction is .11 (7 divided by 64), while the corresponding figure for unsuccessful prediction is 0. From these two columns, I have calculated the two columns of cumulative relative frequencies.

The cumulative frequencies have been plotted in Figure 4. In this diagram, perfect discrimination takes place when the plotted line coincides with the lines framing the diagram. This is because, it would mean that when I predict an incident, it takes place and when I don’t, it does not happen. The 45 degree line shows no predictive discrimination what-so-ever. Hence the area under the cumulative distribution curve in relation to the upper half of the diagram measures the extent of discrimination. Notice that it is the same measure as the Lorenz curve, which is typically used to measure income distribution within a nation. The higher the value of the Lorenz coefficient the better is the predictive discrimination. ₂₉

The problem of using these two relative measures of predictive efficiency is that they present a contradictory picture. Thus, compare Figure 3 with Figure 4. In Figure 3, the best calibrated model will produce predictions along the 45 degree line, while in Figure 4, such a model will be considered as having no discriminating power at all. Therefore, a predictive model must follow a trade-off between the two measures of predictive efficiency.

Correlation:

The third measure of predictive efficiency is correlation. In the standard textbooks “accuracy” may mean “goodness-of-fit,” that is, how well the forecasting model is able to reproduce the data that are already known. For causal analyses (multiple regression models), most researchers use the goodness-of-fit measures. In contrast, for many time-series models, where past data predict the future behavior, a subset of the known data can be used to forecast the rest for the model’s measure of accuracy. Standard statistical measures of goodness-of-fit includes (among others):

Mean Absolute Errors (MAE) =

Mean Squared Errors (MSE) =

or, Mean Absolute Percent Error =

Unfortunately, none of the above measures is free of its own peculiarities and biases. For instance, MAE places equal weight to a slight deviation from the forecast and a huge error. If we want to place a greater significance large false positive or false negative (as we should), then we should square the errors (MSE). Although the objective of statistical optimization is to choose a model which minimizes MSE. However, even its use carries three important reservations.

First, if MSE refers to a time series data, such fittings may not necessarily lead to good forecasting. An MSE of zero can always be obtained by using polynomials of sufficiently high order or an appropriate Fourier transformation. Such overfitting a model to a data series simply internalizes the randomness of the series and does not lend itself toward forecasting the underlying trend. In other words, although we may have a high R-squared value, yet do a lousy job of forecasting.

The second limitation of MSE is that if there are several models using various estimation techniques, the simple comparison of the MSEs will not give us a good enough measure of choosing the best method. This is because different methods use different techniques for fitting data. For instance, smoothing methods are highly dependent upon initial forecasting estimates, standard regression methods minimize MSE by giving equal weight to all observations, Box-Jenkins method minimizes the MSE of a nonlinear optimization procedure.

Finally, unlike the national economic statistics, there is no standard data set that every researcher uses for developing early warning models. In such cases, MSE, being an absolute measure, cannot be used for comparative purposes to determine predictive accuracy when the data sets, time horizons of forecasting and methodologies vary among the forecasters.

In comparison, while having similar shortcomings, the Mean Absolute Percent Error (MAPE), at the very least, has the advantage of simplicity. Since MAPE explains deviations from the forecasts in percentage terms, the result derived from one method can be compared to those obtained from others. Second, it is much more intuitive to the reader if we say that the forecasts, based on method A yields 5% error as opposed to its average mean squared error of 323, for instance.

Makridakis et al. (1985) however, offer yet another method of evaluating forecasting efficiency. They argue that the relative efficiency of intricate (and hence, expensive) models may be judged by setting it against the simplest of all methods of forecasting, the naive forecasts. Naive forecasts simply takes the current period’s value as the predicted value for the future period. The MAPE of naive forecast may be written as:

MAPENF =

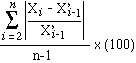
Makridakis, et al. suggest that in order to remove subjectiveness of relative accuracy this measure can be used as the benchmark against which all other the MAPEs of all other forecasting methods can be measured.

Summary

We may summarize our technical discussion with the startling conclusion that the scientific literature fails to provide us with a single, unequivocal measure of predictive efficiency. Even conceptually, predictive efficiency is a relative concept amenable only to trade-offs among various criteria of ideal forecasts. However, when it comes to EW forecasts, we face a far bigger choice in ascertaining relative accuracy of the predicted values. Every measure of accuracy that I have mentioned above is based on one assumed property: The outcomes are independent of the predicted values. For instance, if there is a convincing forecast of an impending disaster, and the government in power takes proper evasive actions to ease tension and/or the world community gets involved in averting it, then the outcome is not independent of the predicted values. Thus, we can confidently claim that if the EW models serve their purpose, there will always be false positive predictions.

 

VI. Regress or not to Regress: Which Method to Use?

In the previous section, I addressed the question: “How do we know that these are good forecasts?” Let us now look at what econometric literature is saying about the relative efficiency of the various methods of forecasting. Consider Figure 1 as the starting point. We would first consider the relative efficiency of causal or econometric models versus time series analyses. Then we will compare forecasts derived from objective methods against those derived from subjective methods.

As the econometric methods were developed and more high speed computing capabilities were available, the decades of 1960s and 1970s, causal forecasting became extremely popular. So much so that a scholar called it the “age of large scale econometric model.” ₃₀ However, the early success of the causal models had great deal a lot to do with the 105 months of uninterrupted economic growth, longer than anytime since 1850. Since econometric models, despite their names, can only measure co-occurrence and do not measure causality, with all the series moving upward, it was relatively easy to find high R-squared values and obtain good forecasts. However, a number of econometricians remained skeptical about the success of causal models as forecasting tools. As early as in 1951, Christ indicated that when structural changes were taking place, causal models were not superior to time-series approaches. Evidence piled up as further studies, using the same data set pitted causal models against time series. Steckler (1968), Cooper (1972), Naylor et al. (1972), Fromm and Klein (1973) all echoed Nelson’s (1972, p. 915) conclusion, “the simple ARMA models are relatively more robust with respect to post sample predictions than the complex (causal) models. Thus if the mean squared error were an appropriate measure of loss, an unweighted assessment clearly indicates that a decision maker would have been best off relying simply on ARMA predictions in the post sample period.” ₃₁

In a provocative article, appropriately entitled, “Forecasting with Econometric Methods: Folklore versus Facts,” Armstrong (1978) surveyed a wide ranging empirical studies and compared forecasts derived from causal models to those obtained from using time-series analysis. He concluded that:

1. Forecasts on the basis of causal analyses were not significantly better than time-series forecasts.
2. In terms of accuracy, complex causal models did not perform better than the simpler causal models.

Having established the fact time-series methods are no inferior to causal analyses, let us look at the effectiveness of forecasts based on econometric models versus the judgmental methods. Econometricians, by and large, are skeptical about the efficacy of expert-based predictions. This is because, expert-based methods, especially the unstructured ones are so closely dependent on seemingly arbitrary (and not articulated) reasoning process of one or more individuals. However, after extensive research where forecasts based on judgmental methods were pitted against those derived from objective econometric analyses, McNees (1982) comes to the following conclusions:

1. There is no tangible proof that forecasts from objective models are generally poor and specifically inferior to judgmental forecasts. At various levels they can perform equally well or equally poorly.
2. Time series forecasts may be more accurate than those derived from causal models in the short term (one period ahead of the current period), but as the time horizon of forecasts increases, the causal models tend to perform considerably better than those of the time series. ₃₂
3. None of the major forecasts are decidedly superior to the others, when one considers difference in various variables or time horizons. Even for a specific variable and time horizon the differences tend to be rather small.
4. However, most importantly, McNees confesses that he is not aware of any test to determine whether the differences are significant in a statistical sense. ₃₃

 

VII. How to Improve Forecast Accuracy? A synergetic Approach

The above discussion points to the fact that there is no single criterion of good forecasts, nor is there a single best method of prediction. Yet, within these constraints, without seeking perfection, we can look for ways to improve the quality of our forecasts. In fact, a great deal of thought has gone into the question of improving accuracy of forecasting. If we look at our broad classification of objective and subjective methods of forecasting, there seems to be good points for both sides.

The advantage of the objective or econometric methods are fairly obvious. When we are dealing with a large amount of data, the underlying patterns of causality is often opaque to a casual observer. The use of statistical method can provide us with precise quantitative estimate of the relative and absolute impact of the independent variables on the dependent variable. However, in political science and especially in the field of studies of catastrophic events, such as genocide and politicide, skepticism about our ability to capture the complex socio-cultural dynamics within the strict structure of econometric modeling is abound. In fact, some have argued that putting analyses within such straight jacket of structured reasoning often leads to “shoddy thinking and the subordination of inquiry to practical utility.” ₃₄

On the other hand, subjective methods, structured or unstructured, can seem chaotic or “seat-of-the-pants” analysis to those seeking objective analysis. It does not require a great deal of statistical insight to know that when forecasts are being conducted on the basis of subjective assessment, it is likely to be influenced by the forecaster’s prejudice, preconceived ideas, ideology and self-interest.

However, cognitive scientists studying information processing within human brains have presented a stronger case for accepting expert-based judgment. For instance, in a provocative work, Nobel Laureate Herbert Simon (1987) has argued that our cognitive structures are well-equipped to handle large number of diverse information is a systematic manner. For instance, the company CEOs or other experts often can come up with intuitive forecasts, which may turn out to be no less accurate than ones derived from more complex mathematical estimation techniques. Political scientists, historians, and students of genocide have put up spirited defense in support of expert analysis. People who have spent the better part of their professional lives studying a particular event, problem, or a region, are in command of a vast array of factual information. Their knowledge of the specifics cannot be overruled by statisticians conducting cross-national studies without the necessary background of the diverse effects unique to each situation. By the very nature of regression analyses, forecasts are weighed toward the average. The experts, in contrast, can make their forecasts specific.

This debate between subjective and objective analysis is not confined within political science or genocide studies. Economists are still embroiled in the controversy. For instance, a Wall Street Journal story reports how important decisions about the future inflation is rate is made by the Federal Reserve Chair, Alan Greenspan. ₃₅ Although the US economy has been able to achieve the enviable position of moderate economic growth with minimal inflation rate for one of the longest economic recoveries in history, spanning nearly 28 quarters, Greenspan has been able to use his uncanny ability to assimilate an incredible amount of quantitative information and pick out the most important ones to forecast the future course of the economy. It is not that his forecasts have always been correct or the path taken has been free of controversy, but the overall achievement speaks for itself. However, skepticism regarding such intuitive method of forecasting remains high despite obvious success. The story quotes Alan Binder, the Vice-Chair of the Federal Reserve saying, “I find it amazing that such good decisions can be made on the basis of numbers like that.” Summing up the sentiment of the objective social scientists, Allan Metzler a noted economist from Carnegie Mellon University states that “I have no fault with the outcome, but we don’t know whether it is hocus pocus.”

The efficacy of expert-based intuitive forecasting has come under scrutiny from psychologists as well. Some time we come across forecasts based on elegant econometric procedures which goes against our own “horse sense.” Should we question the results or since they were derived through a complicated statistical procedure, or should we hold back your doubts? This is an extremely important question, since public policies are based on future expectations. There are a number of highly regarded outfits along with government’s own Office of Management and Budget and the Congressional Budget Office routinely put out forecasts of future economic behavior based on highly complex econometric models. How do the forecasts based on large econometric models compare with the subjective forecasts made by field experts has been the subject of inquiry in recent economic literature. Based on a well-known framework used in psychological research by Egon Brunswick, ₃₆ called the Lens Model, a number of studies have attempted to show the relative reliability of subjective and objective estimations. ₃₇

The empirical results based on controlled experiments show that although subjective estimations appear to be less accurate in the first blush, when the level of structural uncertainty is held constant, both tend to offer forecasts with equal amount of variability. Second, when the subjective forecasts are based on a group consensus, the results tend to show a greater degree of consistency, implying that the group as whole is better able to weed out random disturbances more effectively. Finally, as the field experts gain more experience in forecasting and develop a deeper understanding of statistical analysis, the quality of their subjective forecasts improve. These results point out the need for mutual understanding between statisticians and the field experts in producing better forecasts.

Thus, without much hesitation, we can conclude with Peter Kennedy (1987, p. 207) as follows:

“In general, the idea of combining forecasting techniques is a good one. Research has indicated that the ‘best’ forecast is one formed as an average of a variety of forecasts, each generated by a completely different technique. If the principles on which these different forecasts are based are sufficiently different from one another, an average (or a weighted average, if more confidence is placed in some of these forecasts than others) 38 of these forecasts, called an amalgamated forecast, could prove superior to any single forecasting technique.”

 

VIII. What Have Learned About Forecasting?

In the beginning of the article, I have mentioned two seemingly facetious “golden rules” of forecasting. However, what we have learned from methodological development over the years parallel those “golden rules.”

Reduce our expectations out of social forecasts. Without clairvoyance, it is impossible to predict the future perfectly. This is particularly true of catastrophic events, such as a revolution or genocide and politicide. We must realize that forecasting based on catastrophe theory is still in its infancy. However, while many of these models can be adapted to analyze the past data, their track record in an open system prediction is perhaps no better than those derived from much simpler exercise. For instance, at the time of writing this article, the Serbian regime of Slobodan Miloshevic is under siege from month-long protest demonstrations. Can we predict how it will end up? If it seems that as social scientists we cannot predict these sudden changes (as Kuran would lament), neither can physical scientists in predicting a particular event in an open, complex system. As the river rises, can an engineer predict the exact time a levy is going to break? Can we predict the last snowflake that will start an avalanche?

Therefore, all forecasts have to be stochastic. Like the weather report, when we hear that there is a 50% chance of rain, do we take it mean that it is going to a) rain half the day, b) will it rain every half an hour, c) or, that rain will cover only half the region? In fact, even without the problem of having to decide exactly how much moisture would constitute “rain,” the outcome of a forecast has to be binary; it is either going to rain or not. Rather, we should interpret the report as follows: If the current weather condition prevails, then over many cases similar to this, half will produce rain. Hence, while developing EW models, we should not expect to see exact predictions of specific events.

Forecasts must be continuously updated. A forecast is not an oracular pronouncement. Hence as the external conditions change, so should the predicted values.

The errors of long term forecasts are greater than those of short-term forecasts. In regression analysis, and in fact, in all methods of forecasting, the errors of prediction increases exponentially as we move away in time. Therefore, it is prudent not to make on single long-term prediction and stick by it, but to do series of forecasts with time. We can learn equally from our mistakes as well as from our successes. The FAO, for instance, makes its early warning predictions for crop failure and famine, but does it on a continuous basis; as more data come in, new forecasts are updated (Rashid, 1997).

Forecasts which are used for policy purposes cannot be tested for accuracy. While evaluating a suitable model for EW, we must make the distinction between passive and active forecasting. We may call a forecast passive when it is done for analytical purposes (may be as an academic exercise) or it has no impact on the final outcome. A weather forecast is a passive forecast (since no one does anything about it). On the other hand, when actual outcomes are not independent of the outcomes, we may call them active or policy oriented forecasts. Alas, for policy level forecasts, there is no statistical way of measuring forecasting accuracy. Econometric models, such as the MARMA, is fundamentally based on the assumption of independence between the actual outcomes and their predicted values (Xt and Ft in equation 1). When the two terms are not independent, then we cannot use any standard method of goodness-of-fit. This is clear even at the intuitive level. If forecasts are used for policy purposes, then the final outcomes may reflect either self-fulfilling prophesies or the result of a correction based on the forecasts. For instance, if I alert the inattentive driver of a car that if the car moves along the line it is going right now, it is going to go off the road, and the driver corrects the course. Can I be held responsible for an erroneous forecast? In the Biblical story of Joseph, if his early warning was for a humanitarian crisis for Egypt, then we can point out that that part of his prophesy did not turn out to be true, since the Egyptians did not suffer from famine due to prudent public policy taken by the Pharaoh.

If the effectiveness of early warning forecasts cannot be statistically determined, their efficacy will be discernible in the long run when we compare the number of conflicts in the pre and post-EW periods. In fact, if the EW models serve their purpose, we will only have false positive results.

False positive predictions can also be useful. Even when there are false positive forecasts without any change in policy, they may be of use as consciousness raising tools. For instance, the global environmental early warnings of the Club of Rome in the 1960s have turned out to be false alarms. Yet, the sheer publicity that the shocking study generated created bands of environmentalists. In true sense of the term, the Club of Rome group cannot claim much success as a forecasting exercise. However, looking back, the members can take satisfaction for influencing environmental awareness and changing public policy world wide. After all, this was the true purpose of the project and, in that sense it was of invaluable service to the future of global ecology.

The Devil is in the definition. Experiments in economic forecasting during the early post-War decades were possible because of standardization of macroeconomics data and their collection over a long period of time. Unfortunately, in the area of political and humanitarian crises, there are possibly as many definitions and data sets as there are researchers. With everyone collecting own data sets, there is a significant need for a systematic effort at collecting relevant data. This data set need to be definitionally clear, as accurate as possible and collected over time by agencies which are free of political or ideological biases. Further, there should be continuity with the data set. Without the existence of a standard data set, similar to the Census Bureau or the Commerce Department, we will never be able to determine the relative efficiency of even the passive models of conflict analysis.

Train field observers and workers in data collection and methods of judgmental forecasting. Since predictions based on subjective evaluation can be just as valued as those obtained from using sophisticated forecasting techniques, a lot may be gained by training field observers and NGO workers in ways of evaluating relative risks of future political events.

For best results combine forecasts derived from different sources and methodologies. Research is unequivocal in its finding that amalgamated forecasts yield the best results. An agency developing EW forecasts will do well to gather similar forecasts and then making its own set of forecasts.

Finally, do not fear controversy. Even after collecting meticulous data and conducting sophisticated analyses, debate over the efficacy of EW models is likely to go on for ever. For instance, Kyenes’ The General Theory was published in 1936. After 60 years of experimenting with EW models for policy analysis, the controversy still rages on. For instance, most economists agree that as a result of economic forecasting and anti-cyclical policies, the economy is now more stable that it was in the past. ₃₉ Yet Christina Romer in a provocative yet highly influential series of articles, has challenged this optimistic assessment of the historical record. ₄₀ She argues that the measured reduction in volatility may not reflect an improvement in economic policy and performance but rather an improvement in the economic data. Since the post war data on real GDP and unemployment were poorly calculated, much of the volatility can be attributed to this data collection error. After constructing new data series out of the old ones, Romer finds that the recent period appears much more volatile — indeed, almost as volatile as the early period. Therefore, in constructing EW models, we have a long road ahead and cannot be too impatient about getting rid of forecasting inaccuracies.

 

IX. EW Models: A Few Parting Caveats

In conclusion, I take the position that the complexities of forecasting political and humanitarian crises have been vastly oversold. Although economic forecasting has evolved over half a century, political forecasting is but of recent origin. Therefore, despite skepticism about our ability to develop early warning systems of political and humanitarian crises, we can safely state that although it is difficult to predict the exact nature of the future, it is not impossible to warn nations when they cross the threshold of a safety zone. Only a true random series is totally unpredictable. If there are discernible trends and it is possible to develop causal linkages, then reasonable predictions can be made. In fact, there is hardly any a-priori reason to believe that the unpredictable effects institutional forces are stronger for political forecatings than for other macroeconomic series.

However, there should be yet another caveat. Even under the best of circumstances, there is no necessary link between good forecast and good policy. Hence, we should be extremely cautious about what we can expect from the EW models.

In any case, there should be no doubt about the importance of the task. As professors Gurr and Harff (1996) have pointed out: ethnic hostility remains the most vexing problem for the next century. Therefore, we should acknowledge that the EW models offer one of the best tools for managing future humanitarian and political crises, but at once be realistic and recognize their shortcomings.

 

Bibliography

Alker, Hayward (1994) “Early Warning Models and/or Preventive Information System” in T. Gurr and b. Harff (eds.) “Early Warning of Communal Conflicts and Humanitarian Crises: Proceedings of a Workshop.” Journal of Ethno-Development. Vol. 4, July, pp. 117–123.

Armstrong, J. S. (1978) “Forecasting with Econometric Methods: Folklore versus Facts.” Journal of Business. S1, pp. 549–600.

Atkinson, Stella M. (1979) “Case Study on the Use of Intervention Analysis Applied to Traffic Accident.” Journal of Operations Research Society. Vol. 30, No. 7, pp. 651–59.

Ball, George (1982) The Past Has Another Pattern: Memoirs. New York: W.W. Norton.

Bond, Doug (1997) FRED. Weston, Ma: Virtual Research Associates.

Bond, Doug and Joe Bond (1995) PANDA Codebook. Center for International Affairs. Harvard University.

Bond, Doug, Craig Jenkins, Charles Taylor and Kurt Schock (1996) Contours of Political Conflict: Issues and Prospects for Automated Development of Events Data. Center for International Affairs. Harvard University.

Boutros-Ghali, Boutros (1992) Agenda for Peace. The United Nations. June 17.

Box, G. E. P. and G. M. Jenkins (1976) Time Series Analysis Forecasting and Control. rev. ed. San Francisco: Holden-Day.

Brecke, Peter (1997) “Finding Harbingers of Violent Conflict: Using Pattern Recognition to Anticipate Conflicts.” Conflict Management and Peace Studies. (forthcoming)

Brunswick, Egon (1956) Perception and the Representative Design of Experiments. Berkeley: University of California Press.

Bueno de Mesquita, Bruce (1981) The War Trap. New Haven, CT.: Yale University Press.

Bueno de Mesquita, Bruce (1984) “Forecasting Policy Decisions: An expected utility approach to post-Khomeini Iran” PS. Spring, pp. 226–36.

Bueno de Mesquita, Bruce (1985a) “The War Trap Revisited,” American Political Science Review. Vol. 79, March, pp. 156–77.

Bueno de Mesquita, Bruce, David Newman and Alvin Rabushka (1985b) Forecasting Political Events. New Haven: Yale University Press.

Bull, Hedley (1986) “International Theory: The case for a Classical Approach.” In John A. Vasquez (ed.) Classics of International Relations. Englewood Cliffs, N.J.: Prentice-Hall. P. 93.

Christ, C. F. (1951) “A Test of Econometric Model of the United States, 1921–1974.” Paper presented in Conference on Business Cycles. New York: National Bureau of Economic Research.

Clark, Lance (1983) Early Warning of Refugee Mass Influx Emergencies. Washington D.C.: Refugee Policy Group.

Clark, Lance (1983) Early Warning of Refugee Flows. Washington D.C.: Refugee Policy Group.

Cooper, R. L. (1972) “The Predictive Performance of Quarterly Econometric Models of the United States.” In B. C. Hickman (ed.) Econometric Models of Cyclical Behavior. New York: National Bureau of Economic Research.

Davies, John and Chad K. McDaniel (1993) “The Global Events-Data System” in R. L. Merritt, R. G. Muncaster and D. A. Zines (eds.) International Events Data Developments. Ann Arbor, Mich.: University of Michigan Press.

Davies, John and Chad K. McDaniel (1996) “Dynamic Data for Early Warning and Ethnopolitical Conflict.” Paper presented at International Studies Association, San Diego. Center for Conflict Management and International Development. University of Maryland, College Park, MD.

Duffy, Gavan, Ted R. Gurr, Philllip A. Scrodt, Gottfriend Mayer-Kress and Peter Brecke (1996) “An Early Warning System for the United Nations: Internet or Not.” Mershon International Studies Review. Vol. 39, pp. 315–326.

Dunn, William N. Public Policy Analysis: An Introduction. Second edition. Englewood Cliffs, N.J.: Prentice-Hall.

Fromm, G. and L. R. Klein (1973) “A Comparison of Eleven Econometric Models of the United States.” American Economic Review. May, pp. 385–401.

Gardner, E. S. Jr., and D. G. Dannenbring (1980) “Forecasting with exponential smoothing: some guidelines for model selection.” Decision Sciences. vol. 11, pp. 370–83.

Gerner, Deborah, Philip Strodt, Ronald Fransisco and Judith Weddle (1994) “Machine Coding of Events Using Regional and International Sources.” Vol. 37, pp 91–119.

Gordenker, Leon (1986) “Early Warning of Disastrous Population Movement.” International Migration Review. Vol. 20. No. 2, pp. 170–193.

Gordenker, Leon (1986) “Early Warning: Conceptual and Practical Issues.” in K. Rupensinghe and Michiko Kuroda (eds.) Early Warning and Conflict Resolution. New York: St. Martins Press, pp. 1–15.

Goss, D., and J. L. Ray (1965) “A general purpose forecasting simulator.” Management Science. Vol. 11, No. 6, April, pp. B119–B135.

Granger, C.W.J. (1980) Forecasting in Business and Economics. New York: Academic Press.

Granger, C. W. J. and Paul Newbold (1986) Forecasting Economic Time Series. London: Academic Press. 2nd ed.

Gupta, Dipak K. (1990) The Economics of Political Violence: The Effects of Political Instability on Economic Growth. New York: Praeger.

Gupta, Dipak K. (1994) Decisions by the Numbers. Englewood Cliffs, N. J.: Prentice-Hall.

Gupta, Dipak K., Albert Jongman and Alex Schmid (1994) “Creating A Composite Index for Assessing Country Performance in the Fields of Human Rights.” Human Rights Quarterly. Vol. 16, No. 1, pp.131–62.

Gurr, Ted R. (1970) Why Men Rebel? New Haven: Yale University Press.

Gurr, Ted R. (1993) Minorities at Risk. Washington D.C.: U.S. Institute for Peace.

Gurr, Ted R. and Barbara Harff (1996) Early Warning of Communal Conflicts and Genocide: Linking Empirical Research to International Responses. Tokyo: United Nations University.

Gurr, Ted R. and M. I. Lichbach (1979) “Forecasting of Domestic Political Conflict.” In To Augur Well: Forecasting in Social Sciences. J. David Singer and Michael D. Wallace (eds.) Beverly Hills: Sage.

Gurr, Ted R. and M. I. Lichbach (1986) “Forecasting Internal Conflict: A Comparative Evaluation of Empirical Theories.” Comparative Political Studies. Vol. 19 (April): pp. 3–38.

Gurr, Ted R. and Will Moore (1996) “State versus People: Ethnopolitical Conflict in 1980s with Early Warning Forecasts for the 1990s.” Paper presented to the International Studies Association annual meeting, San Diego, 16–20 April.

Hand, D. J. (1981) Discrimination and Classification. New York: Wiley.

Harff, Barbara (1987) “the Etiology of Genocide” in Michael Dobkowski and Isidor Wallimann (eds.) The Age of genocide. Westport, CN: Greenwood Press, pp. 41–59.

Harff, Barbara (1992) “Recognizing Genocides and Politicides,” in Helen Fein (ed.) Genocide Watch. New Haven: Yale University Press.

Hibbs, Douglas P.Jr. (1973) Mass Political Violence: A Cross-National Causal Analysis. New York: Wiley.

Hibbert, Christopher (1978) The Great Mutiny: India 1857. New York: Viking Press.

Huff, Darrell (1954) How to Lie with Statistics. New York: W. W. Norton Co.

Kennedy, Peter (1987) A Guide to Econometrics. Second edition. Cambridge, Mass. MIT Press.

Kirby, R. M. (1966) “A Comparison of Short and Medium Range Statistical Forecasting Method.” Management Science. No. 4, pp. N202–B210.

Kmietowicz, Z. W., and H. Ding (1993) “Statistical Analysis of Income Distribution in the Jiangsu Province of China.” The Ststistician. Vol. 42, No. 2, pp. 107–121.

Kuran, Timur (1993) “Mitigating the Tyranny of Public Opinion: Anonymous Discourse and the Ethic of Sincerity.” Constitutional Political Economy. Vol. 4. No. 1, 1993.

Kuran, Timur (1995a) “The Inevitability of Future Revolutionary Surprises.” American Journal of Sociology. Vol. 100, No. 6. Pp. 1528–1551.

Kuran, Timur (1995b) Private Truths, Public Lies. Cambridge: Harvard University Press.

Levine, A. H. (1967) “Forecasting Technique” Management Accounting. January.

Lichbach, Mark I. (1985) “Protest in America: Univariate ARIMA Models in Post-war Era.” Western Political Quarterly. 38 (September): 581–608.

Makridakis, S. and M. Hibon (1982) “The accuracy of forecasting: An empirical investigation” Journal of Royal Statistical Society, pp. 97–145.

Makridakis, Spyros, Steven C. Wheelwright, and Victor E. McGee (1983) Forecasting: Methods and Applications. New York: John Wiley.

Mankiw, N. Gregory (1997) Macroeconomics (Third Edition); New York: Worth Publishers.

Marshall, Kneal T. And Robert M. Oliver (1995) Decision Making and Forecasting. New York: McGraw-Hill, Inc.

McLachlan, G. J. (1992) Discriminant Analysis and Statistical Pattern Recognition. New York: Wiley.

McNees, S. K. (1982) “The role of Macroeconometric Models in forecasting and policy analysis in the United States.” Journal of Forecasting. Vol. 1. January.

Murphy, A. H. and R. L. Winkler (1992) “Diagnostic Verification of Probability Forecasts.” International Journal of Forecasting. Vol. 7, pp. 435–55.

Naylor, T. H., T. G. Seaks and D. W. Wichern. (1972) “Box-Jenkins Methods: An Alternative to Econometric Forecasting.” International Statistical Review. Vol. 40, No. 2., pp. 123–37.

Nelson, C. (1972) “The Prediction Performance of the FRB-MIT-PENN Model of the U.S. Economy. American Economic Review. Vol. 62, No. 5. December, pp. 902–17.

Nelson, T. O. (1986) “ROC Curves and Measures of Discrimination Accuracy: A Reply to Swets.” Psychological Bulletin. Vol. 100, pp. 128–32.

Newbold, Paul (1973) “Bayesian Estimation of Box-Jenkins Transfer Function-noise Models.” Journal of Royal Statistical Society. vol. 35, No. 2, pp. 323–36.

Newbold, Paul and C. W. J. Granger (1974) “Experience with forecasting univariate time series and the combination of forecasts.” Journal of the Royal Statistical Society, Series A, 137, part 2, pp. 131–65.

Raine, J. E. (1971) “Self-Adaptive Forecasting Considered,” Decision Sciences, April. Romer, Christina (1986a) “Spurious Volatility in Historical Unemployment Data.” Journal of Political Economy. Febrary. pp. 1–37.

Rashid, Abdur (1997) “Averting Famine through Linking Early Warning with Response Mechanism.” Paper presented at the Synergy in Early Warning Research Conference. Toronto, Canada.

Rao, U. L. G. And A. Y. P. Tam (1987) “An Empirical Study o Selection and Estimation of Alternative Models of the Lorenz Curve.” Journal of Applied Statistics. Vol. 14, pp. 275–80.

Romer, Christina (1986a) “Spurious Voaltility in Historical Unemployment Data,” Journal of Political Economy. Vol. 94, February, pp. 1–37.

Romer, Christina (1986b) “Is the Stabilization of the Postwar Economy a Figment of the Data?” American Economic Review. June, pp. 314–334.

Rosenthal, A. (1989) “Broad Disparities in Votes and Polls Raising Questions,” New York Times, November 9, 1989, pp. A1, B14.

Rupensinghe, Kumar and Michiko Kuroda (eds.) Early Warning and Conflict Resolution. New York: St. Martins Press.

Schmeidl, Susanne and J. Craig Jenkins (1997) “The Early Warning of Humanitarian Diasters: Problems in Building an Early Warning System.” International Migration Review (forthcoming).

Schmid, Alex P. and Albert Jongman (1997) “Mapping Violent Conflicts and Human Rights Violations in the Mid-199’s: Assessing Escalation and De-Escalation — PIOOM’s Approach.” Synergy in Early Warning. Susanna Schmeidl and Howard Adelman (eds.) York University, Toronto, pp 301–22.

Schrodt, Philip and Deborah Gerner (1994) “Validity Assessment of Machine-Coded Events Data Set for the Middle East, 1982–1992” American Journal of Political Science. Vol. 18, pp. 132–56.

Schrodt, Philip (1995) KEDS: Kansas Events Data System. Dept. of Political Science, University of Kansas, Lawrence, KS.

Schrodt, Philip (1997) “Pattern Recognition of International Crises Using Hidden Markov Models.” Paper presented at the annual meeting of the International Studies Association, Toronto; and Synergy in Early Warning Conference, Centre for Refugee Studies, York University, Toronto.

Simon, Herbert (1987), “Making Management Decisions: The Role of Intuition and Emotion.” Academy of Management Executive, vol. 1, #1, pp. 57–64.

Singer, J. David and Michael D. Wallace (eds.) To Augur Well: Forecasting in Social Sciences. Beverly Hills: Sage.

Singh, Harinder (1990) “Relative Evaluation of Subjective and Objective Measures of Expectations Formation” Quarterly Review of Economics and Business, vol. 30, No. 1, pp. 64–74.

Steckler, H. O. (1968) “Forecasting with Econometric Models: An Evaluation.” Economterica. Vol. 34. July–October, pp. 437–63.

Swets, J. A. (1986) “Indices of Discrimination or Diagnostic Accuracy: Their ROC and Implied Models.” Psychological Bulletin, Vol. 99, No. 1, pp. 100–117.

The Wall Street Journal, Monday, January 27, 1997, p. 1 “Choosing A Course: In Setting Fed’s Policy, Chairman Bets Heavily on His Own Judgment. Greenspan Loves Statistics, But Uses Them In A Way That Puzzle Even Friends. Some Forecasts Go Awry.”

Tilly, Charles (1978) From Mobilization to Revolution. Reading, MA: Random House.

Thomas, P. (1990) “The Persistent ‘Gnat’ that Louisiana Can’t Get Out of Its Face,” Los Angeles Times, October 14, 1990, p. M1.

Urkowitz, H. (1983) Signal Theory and Random Processes. Artech House, Dedham, MA.

West, C.T. and Fullerton, T. (1996) “Assessing the Historical Accuracy of Regional Economic Forecasts,” 1996, Journal of Forecasting 15, 19–36.

Wilkie, A. D. (1992) “Measures for Comparing Scoring Systems.” In L. C. Thomas, J. N. Crook, and D. B. Edelman (eds.) Proceedings of a Conference on Credit Scoring and Credit Control. Oxford: Oxford University Press, pp. 123–38.

 

---

Endotes

Note 1: Quoted in Georgie Anne Geyer (1997) “Control the media and Win Bosnia” San Diego Union Tribune. Monday, November 24, p. E3. Back.

Note 2: I am particularly grateful to Professors Ted Gurr, Barbara Harff and Timur Kuran for their comments on the earlier version of this paper. Also, I thankful to Craig Jenkins, Serge Rey and Jim Gerber for their suggestions. The remaining errors reflect my own shortcomings. Back.

Note 3: Ted R. Gurr and Barbara Harff (1996) p. 9. Back.

Note 4: See, for example, Alker (1994). Back.

Note 5: For example, see Timur Kuran (1995a) “The Inevitability of Future Revolutionary Surprises.” American Journal of Sociology. Vol. 100, No. 6. Pp. 1528–1551. Back.

Note 6: History is repleat with examples of small events causing large outcomes. For example, in 1857, the British colonial rule in India was shaken up by a widespread mutiny by the Indian “Sepoys.” The immediate cause of the rebellion was the introduction of a new kind of rifle. For these weapons, the cartridges had to be prepared with grease. Rumor strated spreading that the grease contained cow (sacred to the Hindus) and pig (forbiddent to the Muslims) fat. At first, the incident was considered to be of little importance. Captain J. A. Wright, an European officer reported that;” There apprears to be a very unpleasant feeling existing among the native soldiers who are here for instruction, regarding the grease used in preparing the cartridges, some evil disposed persons having spread a report that it consists of a mixture of the fat of pigs and cows. ... I assured them (believing it to be the case) that the grease used is composed of mutton fat and wax.” From this relatively small incident, within a matter of months, the entire British India of nearly 150 millin then, was soon engulfed in the flames of a huge rebellion. See, Christopher Hibbert (1978, p. 63). Back.

Note 7: See, Kuran (1995b) pp. 247–60. Back.

Note 8: Ted R. Gurr and Barbara Harff (1996), op cit. p. 9. Back.

Note 9: See C.W.J. Granger (1980). Back.

Note 10: See G. E. P. Box and G. M. Jenkins (1976) Time Series Analysis Forecasting and Control. rev. ed. San Francisco: Holden-Day. For application, see Stella M. Atkinson (1979) “Case Study on the Use of Intervention Analysis Applied to Traffic Accident.” in Journal of Operations Research Society. Vol. 30, No. 7, pp. 651–59. Back.

Note 11: For a detailed explanation see, Makridakis et al. (1983), Newbold (1973). Back.

Note 12: For instance, in his autobiography, George Ball, the former Undersecretary of State in the Kennedy and Johnson administrations, narrates how crucial decisions during the Vietnam war were taken on the basis of subjective probabilities of success given by Robert McNamara, then Secretary of Defense (see Ball, pp. 173–74). Back.

Note 13: See Darrell Huff (1954). Back.

Note 14: For example, in the 1990 U.S. Senate election in Louisiana, the Democratic candidate was widely predicted to score an overwhelming victory over David Duke, a former grand wizard of the Ku Klux Klan whose platform rested on opposition to affirmative action. Pre-election polls projected that Duke would garner no more than 25% of the votes. Yet when the actual poll results were tabulated, he had managed to get 44%, including 60% of the white votes (see P. Thomas, 1990). Even the exit polls turned out to be in accurate, suggesting that many people would not admit to having voted for Duke. Similarly, on the eve of the 1989 mayoral election in New York, polls gave David Dinkins, an African-American candidate, a 14 to 18% lead over Rudolph Guiliani (who is white). the exit polls predicted a 6 to 10% spread between the candidates. However, the actual margin of win turned out to be much smaller, a meager 2% margin. (see A. Rosenthal, 1989 for the news report. For analysis see Timur Kuran, 1993). Back.

Note 15: For a detailed description of the various efforts, see Gurr and Harff (1996) and Schmeidl and Jenkins (1997). For relevant discussion, see Singer and Wallace, 1979; Clark, 1983, 1989; Gordenker 1986, 1992; Rupensighe and Kuroda 1992; Duffy et al. 1996; Schrodt and Gerner, 1996; Davis and McDaniel 1996). Back.

Note 16: See, Douglas P. Hibbs (1973); Gupta (1990); Lichbach (1996). Back.

Note 17: See, for instance, Lichbach (1985). Back.

Note 18: See Singer and Wallace (eds. 1979), especially Gurr and Lichbach. Back.

Note 19: See Gurr and Harff (1996). Ch. 3, p. 46. Back.

Note 20: A comprehensive list in this area is naturally too extensive to mention in a footnote. For a representative sample, see Bruce Bueno de Mensquita (1981, 1985a). Back.

Note 21: Bueno de Mesquita, David Newman and Alvin Rabushka (1985) p.16. Back.

Note 22: See Dipak K. Gupta (1994). Back.

Note 23: See for example, Bueno de Mesquita, David Newman and Alvin Rabushka (1985). Back.

Note 24: See, Kneal T. Marshall and Robert M. Oliver (1995), especially, Ch. 8, pp. 303–339. Back.

Note 25: For an example of actual use of such measures, see Schmid and Jongman (1997). Although Schmid and Jongman used slightly different measures of political crisis. Back.

Note 26: In symbolic terms, it is written as:
E[F] = E[X]

when

Back.

Note 27: This diagram is obtained by plotting the “probability of actual event” (column 4 in Table 2) as the X axis and the “probability of predicted events” (column 5 in Table 2) as the Y axis. Back.

Note 28: The problem of calibration has been widely used in the decision theory and forecasting literature, coving a myriad subjects. For instance, see Nelson (1986), Swets (1986), Rao and Tam (1987), Wilkie (1992) and Kmietowicz and Ding (1993). For a theoretical discussion, see Urkowitz (1983). Back.

Note 29: Most forecasting studies depend on either calibration or correlation. A relatively small number of studies use discrimination. For example, see Hand (1981), McLachlan (1992), Nelson (1986), Murphy and Winkler (1992). Although relatively few studies use discrimination as a criterion for forecasting accuracy, the concept of discrimination is the basis of discriminant analysis, a widely used multivariate technique in social sciences and psychology. For an example of building cross-national human rights performance by using discriminanat analysis, see Gupta, Jongman, and Schmid (1994). Back.

Note 30: See Naylor et al. (1972). Back.

Note 31: “Post sample period” means outside the currently available data, looking into the future. For similar conclusions, see, Kirby (1966), Levine (1967), Gross and Ray (1965), Raine (1971), Gardner and Dannenbring (1981), Newbold and Granger (1974) Makridakis et al. (1982). Back.

Note 32: However, we should recall that as the time horizon of forecasts outside of the sample set increases, the standard error of forecasts increases exponentially, thereby limiting the efficacy of the causal models. Back.

Note 33: For a similar conclusion, see, C. T. West and T. Fullerton (1996). Back.

Note 34: Hedley Bull (1986). In this context, also see Alker (1994). Back.

Note 35: The Wall Street Journal, Monday, January 27, 1997, p. 1 “Choosing A Course: In Setting Fed’s Policy, Chairman Bets Heavily on His Own Judgment. Greenspan Loves Statistics, But Uses Them In A Way That Puzzle Even Friends. Some Forecasts Go Awry.” Back.

Note 36: Egon Brunswick (1956) Perception and the Representative Design of Experiments. Berkeley: University of California Press. Back.

Note 37: See, Harinder Singh (1990) “Relative Evaluation of Subjective and Objective Measures of Expectations Formation” Quarterly Review of Economics and Business, vol. 30, No. 1, pp. 64–74. Back.

Note 38: Notice the introduction of yet another dose of subjective assessment. Back.

Note 39: See, for instance, Mankiw (1997) pp. 369–70. Back.

Note 40: Romer (1986a; 1986b) Back.

Early Warning and Early Response