email icon Email this citation

CIAO DATE: 02/01

The Paradox of Disconnected Coalitions 1

Steven J. Brams *
Michael A. Jones **
D. Marc Kilgour ***

International Studies Association
41th Annual Convention
Los Angeles, CA.
March 14-18, 2000

Abstract

The paradox of disconnected coalitions is that "disconnected" coalitions can arise from the "connected" (i.e., single-peaked) preferences of as few as five or six players. Two models of coalition formation are analyzed in which the paradox can occur, in both of which players coalesce when they all find each other mutually acceptable:

FB better reflects the unconstrained, or nonmyopic, possibilities of coalition formation, whereas BU, because all subcoalition members must be included in any majority coalition that forms, restricts combinatorial possibilities considerably and tends to produce larger and less tight majority coalitions.

If player perceptions of the single-peaked ordering are sufficiently similar ("spatially" single-peaked), the paradox is precluded. But the strange bedfellows frequently observed in legislative coalitions and military alliances suggest that even when players agree on, say, a left-right ordering, their perceptions of exactly where players stand in this ordering may differ substantially. In such situations a player, while acceptable to a coalition, might not find every member in it acceptable, which causes that player not to join and creates a "hole" in an otherwise connected coalition. Applications of the models are discussed.

JEL Classification: C61, C78, D72

Keywords: Coalition formation; dynamic analysis; single-peakedness; legislatures; military alliances.

1. Introduction

That individual coherence, like transitive individual preferences, can lead to social incoherence, like the Condorcet paradox of cyclical majorities, is well-known in the social-choice literature. What is less well-known is that this phenomenon can arise in coalition formation.

In this paper, we show how "connected" preferences can create "disconnected" coalitions, giving rise to the "paradox of disconnected coalitions" in two simple models of coalition formation. In the first, each player either ranks or rates every other player in terms of that player's desirability as a coalition partner. Players progressively descend in their preference rankings or ratings until there is a simple majority of members that considers every other member of that majority acceptable as a coalition partner. 2

Before the descent reaches a level at which there is such a majority, smaller coalitions, or subcoalitions, whose members find each other mutually acceptable, may form. If these subcoalitions do not constrain the coalition-formation process–in the sense that coalitions that form later must contain all members or no members of any subcoalition that formed earlier–we call the coalition-formation process unconstrained.

By contrast, we call coalition formation constrained if subcoalitions, as soon as they form, fuse into composite players whose preferences reflect those of their component members. Treating these composite players as single players–whose component members can no longer be separated–in a smaller game, we repeat the descent process until new subcoalitions form. This process continues until a majority coalition forms, whose individual and composite players all consider each other mutually acceptable.

Whether constrained or unconstrained, we assume the descent in player preferences or ratings proceeds according to the rules of "fallback bargaining" (Brams and Kilgour, 1999), which we describe and illustrate in section 4 in the context of coalition formation. In addition, we make the following assumptions about preferences. They are single-peaked if

More stringently, preferences are spatially single-peaked if

The paradox of disconnected coalitions is that the first majority coalition to form under either unconstrained or constrained coalition formation may be disconnected if preferences are single-peaked, but not if they are spatially single-peaked. To illustrate a disconnected coalition, assume that six players can be ordered 1-2-3-4-5-6 along a left-right dimension. Then the first majority coalition to form might be {1, 2, 3, 5}–without player 4–creating a "hole" in an otherwise connected coalition.

This seems paradoxical, because if any individual player considers both players 3 and 5 desirable as coalition partners, single-peakedness implies that it must also consider player 4 desirable. Indeed, if preferences are single-peaked, the preferred coalition partners of each player will form a cluster, without holes, around that player. Yet these connected individual preferences of players can result in a disconnected majority coalition (i.e., with holes) if player preferences are single-peaked. 3

The minimum number of players required for a disconnected coalition to be the first to form is five or six, depending on the model of coalition formation assumed, which is well above the minimum of three players required to demonstrate the Condorcet paradox. While these disconnected coalitions always minimize the maximum distance between any two members of the coalition, the resulting coalitions may not be "tight" in a sense to be defined later.

The paper proceeds as follows. In section 2, we distinguish between single-peaked and spatially single-peaked preferences, showing in what sense the latter are consistent but the former are not. In section 3, we show that there may be no stable majority coalition, whether preferences are single-peaked or spatially single-peaked.

In the absence of such a stable outcome, we focus on the process of coalition formation, analyzing what we call fallback, or unconstrained, coalition formation in section 4. We demonstrate that the paradox of disconnected coalitions can occur with as few as six players.

In section 5, we show how preferences can be quantified, which paves the way for introducing a measure of cardinal rather than ordinal distance. With cardinal distances, the minimum number of players required to produce the paradox drops from six to five.

The build-up, or constrained, model is introduced and analyzed in section 6. While it tends to produce larger majority coalitions than the fallback model, it, too, can lead to disconnected coalitions with as few as five players.

We present our conclusions in section 7, emphasizing the importance of analyzing the dynamics of coalition formation rather than just looking for stable outcomes, which are generally nonexistent except under quite restrictive assumptions. In addition, we comment on the applicability of the models to coalition formation in legislatures. Finally, we briefly discuss the formation of military alliances in World Wars I and II, focusing on the apparently disconnected Axis alliance in World War II.

2. Single-Peaked and Spatially Single-Peaked Preferences

Preferences are said to be single-peaked if there exists an ordering of players, along a single dimension, such that, for each player, its more-preferred coalition partners are always closer to it than its less-preferred coalition partners. Hence, its more-preferred partners form a cluster around it, as we will illustrate shortly.

That this is not always possible is illustrated by the standard three-person example of the Condorcet voting paradox, wherein we assume that players, instead of ranking alternatives, rank each other as coalition partners:

Thus, player 1's first choice of a coalition partner is player 2, and its second choice is player 3. While we do not include playeri in its own ranking, implicitly we assume that player i ranks itself highest–that is, it most desires that it be included in any majority coalition that forms.

It is straightforward to check that no ordering of the players along a single dimension, going from left to right, such as

can be consistent with the preferences of players in Example A. For instance, the above ordering is consistent with the rankings of players 1 and 2, but not with the ranking of player 3, because player 3 prefers player 1 to player 2 as a coalition partner, whereas the above ordering implies the reverse preference. None of the five other orderings of players 1, 2, and 3 (there are 3! = 6 different orderings) is consistent with all three players' preferences in Example A.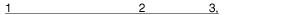

While single-peakedness requires only that each player's preference be describable by the same left-right ordering of players, there is no requirement that each player has exactly the same perception of the positions of all players, and therefore of the distances between them. Indeed, it may be necessary for the players to have different perceptions of the distances, as illustrated in our next example (with order 1-2-3-4):

Because player 2 ranks player 1 last as a coalition partner, player 2 (in boldface below) must perceive that the distance between it and adjacent player 1 is greater than the distance between it and adjacent player 3, or for that matter between it and nonadjacent player 4: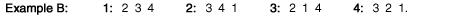
By comparison, because player 3 ranks player 4 last as a coalition partner, player 3 must perceive that the distance between it and adjacent player 4 is greater than the distance between it and adjacent player 2, or for that matter between it and nonadjacent player 1, as illustrated below: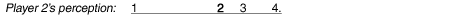

We say that players' preferences are spatially single-peaked if it is possible to describe them by a single spatial model of player positions along the real number line. Assume that player i's position on this line is xi , and player j's position is xj , so that the distance between them is. Then player i's preference ordering for coalition partners is given by ranking i first, followed by all other players, j, in increasing order of dij . 4

We adopt the convention that players with single-peaked preferences are named in such a way that their ordering is, from left to right, 1, 2, 3, . . ., n. Note that player 1's preference ordering must be 1: 2 3 4 . . . n, and player n's must be n: n-1 n-2 . . . 1. We also assume, for convenience, that two or more players are never equally preferred, by being equally distant–either to the left or the right–of any player i.

It is easy to see that if players' preferences are single-peaked, and if f is any integer satisfying 1 < f < n, then player i's f most-preferred coalition partners, including i itself, is the subset {g(i), g(i) + 1, . . ., h(i)}, where and g(i) < i < h(i) and h(i) = g(i) + f - 1. That is, player i's most-preferred set of coalition partners forms a cluster, without "holes," around player i. For instance, set f = 3 in Example B. Then each player's three most-preferred coalition partners, listed from left to right, are as follows:

It can be checked that when preferences are not single-peaked, then any linear ordering of the players (i.e., along a line) must result in some player's set of f most-preferred coalition partners, for some f, having a hole. In Example A, for instance, when the linear ordering is 1-2-3, player 3's two most-preferred coalition partners are {1, 3}, leaving a hole because of the absence of player 2.

If preferences are spatially single-peaked, on the other hand, then the clusters around each player have the following monotonicity property: For any f, i < j implies that g(i) < g(j) 5 . In words, if player i is to the left of player j, then the set containing player i's f most-preferred coalition partners must either be identical to player j's or start to the left of j's. 6

To illustrate, consider the following example, in which player preferences are spatially single-peaked:

If f = 3, the most-preferred sets of coalition partners, again listed from left to right, are: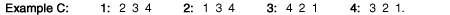
Notice that (i) player 1 and 2's, and player 3 and 4's, most-preferred sets of coalition partners are identical and (ii) player 2's most-preferred set starts with player 1, one position to the left of the starting player (i.e., 2) in player 3's most-preferred set, satisfying monotonicity.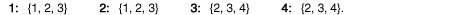

By contrast, the most-preferred sets in Example B, in which preferences are single-peaked but not spatially so, do not satisfy this property: Player 2's most-preferred set starts with player 2, one position to the right (not the left) of the starting player (i.e., 1) in player 3's most-preferred set.

Our results so far can be summarized as follows:

  1. If preferences are not single-peaked, as in Example A, they cannot be described by a single linear ordering, which means that there are "holes," with respect to any linear ordering of the players, in the set of the most-preferred coalition partners of some players.
  2. If players' preferences are single-peaked, as in Example B, there is such a linear ordering, so each player's most-preferred coalition partners form a cluster around its preferred position.
  3. If preferences are spatially single-peaked, as in Example C, player positions are describable by a single spatial model, rendering players' perceptions of distance consistent. Such consistency implies the following monotonicity property: If player i's position is to the left of player j's, then i's set of most-preferred coalition partners may not start to the right of j's. 7

3. Stable Majority Coalitions: They May Not Exist

If preferences of players for coalition partners are not single-peaked, it is no surprise that there do not exist stable majority coalitions. To see this in Example A, consider simple-majority coalition {1, 2}, which we write as 12. Because player 2 would prefer to be in coalition 23 since it ranks player 3 higher than player 1 as a coalition partner, 12 is unstable–there is a different majority coalition that one of its members would prefer. Likewise, the other simple-majority coalitions, 13 and 23, are unstable. 8

Assume that each player least prefers the two-person coalition of which it is not a member. Then the players will rank the three possible two-person coalitions as follows:

Observe that a majority (players 1 and 2) prefers 12 to 13, a majority (players 1 and 3) prefers 13 to 23, and a majority (players 2 and 3) prefers 23 to 12. Letting ">" signify majority preference, we have 12 > 13 > 23 > 12, so majority preferences over coalitions cycle, a problem that far-sightedness does not solve (Chakravorti, 1999).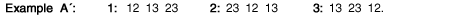

What is more surprising is that greater preference consistency does not solve the stability problem:

Proposition 1. If preferences are single-peaked, there may be no stable majority coalition.

Proof. Consider Example B, where player preferences are single-peaked with respect to ordering 1-2-3-4. 9 Now consider majority coalition 123. Player 2 would prefer to be in coalition 234 because it ranks player 4 higher than player 1 (both coalitions share players 2 and 3); hence, coalition 123 is unstable. Likewise, majority coalition 234 is unstable, because player 3 has the opposite preference–it prefers player 1 to player 4. Finally, in the case of the two disconnected majority coalitions, 124 and 134, it is easy to show that all three players would each prefer to be in one or the other of the connected coalitions, 123 and 234. Q.E.D.

In Example B, preferences are single-peaked but not spatially single-peaked. As we showed in section 2, players 2 and 3 have different perceptions of the distances between players, even though they both perceive the left-right ordering of the players to be the same. But the lack of a single spatial representation of distance for all players is not the only reason for coalitions to be unstable. Even spatially single-peaked preferences are insufficient to ensure coalitional stability, leading to a strengthening of Proposition 1:

Proposition 2. If preferences are spatially single-peaked, there may be no stable majority coalition.

Proof. Consider Example C, whose player preferences, we showed in section 2, are spatially single-peaked. It is not difficult to show that the players' perceptions of distance are consistent and can be represented as follows: 10

Now consider majority coalition 123. Because player 3 would prefer to be in coalition 234 since it ranks player 4 higher than player 1 as a coalition partner (both coalitions share players 2 and 3), coalition 123 is unstable. Likewise, coalition 234 is unstable, because player 2 would prefer to be in coalition 123 than 234. Finally, all three players in the disconnected coalitions, 124 and 134, would prefer to be in one of the connected coalitions, 123 or 234. Q.E.D.

Thus, neither single-peakedness nor the stronger property of spatial single-peakedness, in which players' perceptions of distance satisfy the monotonicity property that renders them consistent, is sufficient to prevent coalitional instability: There may be one or more coalition members that would prefer to be in a different majority coalitions.

Some differences in these examples are worth noting. In Example B, player 3 prefers coalition 123 to coalition 234, even though player 3 is an endpoint, dimensionally speaking, of coalition 123 (see the representation of player 3's perception in section 2). In Example C, while player 3 is the midpoint in coalition 234 and would also prefer it to coalition 123, notice that coalition 123 is a "tighter" coalition than coalition 234 in the sense that the distance separating the endpoints of 123 is less than that separating the endpoints of 234 (see the representation of all players' perceptions in the proof of Proposition 2). Because a tighter coalition is more likely to be stable, player 3 might therefore consider coalition 123 more desirable than coalition 234. In section 5, we will discuss tightness in cardinal terms after analyzing it, ordinally, in the section 4.

To sum up, because player preferences are not single-peaked in Example A, majority coalitions are expectedly unstable. More unexpectedly, in single-peaked Example B, and even in spatially single-peaked Example C, every majority that forms will have one or more players that would prefer to be in a different majority coalition. Single-peakedness, in both a weak and strong (spatial) sense, is therefore insufficient to guarantee coalitional stability. 11

4. Fallback (Unconstrained) Coalition Formation: The Paradox

If instability plagues majority coalitions even when preferences are spatially single-peaked, it is appropriate to turn to models of coalition formation to try to explain why certain majority coalitions form rather than others. The dynamic process by which they do so may lend stability to the majority coalition that ultimately emerges, even if some members have an incentive to defect, as illustrated in our preceding examples.

Disconnected coalitions would appear to be especially vulnerable. To demonstrate the paradox of disconnected coalitions, we first define and illustrate fallback coalition formation (FB), in which no constraints are placed on what majority coalitions may form by the subcoalitions that form prior to their emergence. FB proceeds as follows:

  1. The most desirable coalition partner of each player is considered. If two players mutually desire each other, and this is a majority of players, then this is the majority coalition that forms. The process stops, and we call this a level 1 majority coalition.
  2. If there is no level 1 majority coalition, then the next-most desirable coalition partners of all players are also considered. If there is a majority of players that mutually desire each other at this level, then this is the majority coalition (or coalitions) that forms. The process stops, and we call this a level 2 majority coalition.
  3. The players descend to lower and lower levels in their rankings until a majority coalition, all of whose members mutually desire each other, forms for the first time. The process stops, with the resulting largest majority coalition(s) that form at this level designated FB coalition(s).

We illustrate FB with the preceding examples:

There is no level 1 majority coalition, because no pair of members consider each other mutually desirable at this level. At level 2, however, the grand coalition (of all players), 123, forms, because members of all pairs, 12, 13, and 23, become mutually desirable at this level, which implies the grand coalition. Thus, FB produces no simple-majority (i.e., two-person) coalition; instead, the FB coalition is the grand coalition.

At level 1, coalition 23 forms; at level 2, coalitions 13 and 24 form; at level 3, coalitions 12, 14, and 34 form, as well as all 3-person coalitions and the grand coalition, 1234. As in Example A, FB produces no simple-majority (i.e., three-person) majority coalition but instead the grand coalition. Unlike Example A, however, majority preferences do not cycle:

Players 2 and 3 are said to be in a top cycle, whereby they can defeat other players (1 and 4) in pairwise contests but not each other. 12

At level 1, coalitions 12 and 34 form; and at level 2, coalition 23 forms; at level 3, coalitions 13, 14, and 24 form, as well as all 3-person coalitions and the grand coalition, 1234. As in Example B, FB produces no simple-majority (i.e., three-person) majority coalition, majorities do not cycle, and there is no unique Condorcet player (players 2 and 3 tie 2-2 against each other, but only player 2 beats player 1 and only player 3 beats player 4).

In single-peaked Example B and spatially single-peaked Example C, all the two-person coalitions that form at levels 1 and 2 are of adjacent players along the 1-2-3-4 dimension. We next present a six-person example in which a coalition–in fact, the first majority coalition to form under FB, and hence the unique FB coalition–includes nonadjacent players along a 1-2-3-4-5-6 dimension, proving the following proposition:

Proposition 3. If preferences are single-peaked, an FB coalition may be disconnected.
Proof. Assume six players are positioned along a left-right dimension 1-2-3-4-5-6, with their single-peaked preferences as follows:
Example D (Paradox of Disconnected Coalitions)

One can verify that these preferences are single-peaked by checking that each player's acceptable coalition partners, for every f, cluster around it without holes, but they are not spatially single-peaked. 13

The largest coalitions that form at each level–with no smaller coalitions as subsets 14 –until a single FB coalition forms at level 4, are as follows (the starred coalitions will be explained after the next example):

Clearly, FB coalition 1235 is disconnected, with a hole due to the absence of player 4. The underlying reason that player 4 is excluded from coalition 1235 is that whereas players 1, 2, and 3 necessarily rank player 4 higher than player 5 (because of single-peakedness), player 4 ranks players 3, 2, and 1 at the bottom of its preference order. In particular, player 4 does not consider player 1 acceptable at level 4, which precludes coalition 1234 (and, hence, coalition 12345) from forming at this level.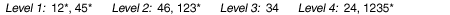
Proposition 4. If preferences are single-peaked, a 6-person example is the minimal example of a unique disconnected FB coalition.

Proof. For players 1 and n to be in the same coalition, the descent must reach the bottom level (i.e., n - 1), because player 1 ranks player n last and vice versa. But at level n - 1, the (connected) grand coalition forms. Because disconnected majority coalitions when n = 3 (two members) and n = 4 (three members) must include the extreme players, 1 and n, such a coalition cannot form until level n - 1, when the grand coalition also forms.

When n = 5, the only possible disconnected majority coalitions are 124, 245, 134, and 235, because disconnected coalitions that contain four members must include both members 1 and 5, which implies a descent to level n - 1 when the grand coalition forms. By symmetry of the left-right ordering, the coalitions 124 and 245 are equivalent, as are the coalitions 134 and 235, so we need consider only the former coalitions in each case.

The coalition 124 can form only at level 3, because player 1 has preference ordering 1: 2 3 4 5. Assume that coalition 124 forms at level 3 and no majority coalition forms at level 2, which would necessarily be connected. We will show that a connected coalition must form at level 3, too.

Player 4 must have preferences 4: 3 2 1 5 for coalition 124 to form at level 3. And player 2 must have player 5 bottom-ranked. Since player 3 can only have player 1 or player 5 bottom-ranked, player 3 must rank players 2 and 4 by level 3.

From the foregoing restrictions on player preferences, the coalition 234 must form by level 3. Moreover, if player 3 has player 5 bottom-ranked, then the coalition 1234 forms at level 3 as well, subsuming coalitions 124 and 234. Either way, the disconnected coalitions 124 is not the unique majority coalition to form at level 3.

An analogous argument shows that coalition 234, and possibly coalition 1234, must form at the same level as the disconnected coalition 134. Q.E.D.

Define a tight k-coalition to be a coalition with k members that requires the fewest pairwise switches in ranks to render its members mutually acceptable and top-ranked choices. These coalitions are starred in 6-person Example D earlier (in the proof of Proposition 3) and in 5-person Example E below: 15
Example E

In this example, the largest coalitions that form at each level, until FB coalition 234 forms at level 3, are as follows: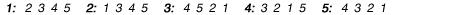

To illustrate the concept of tightness, notice that 2-coalition 14 in Example E forms at level 3, which is the first level in the descent at which player 1 considers player 4 desirable. It would therefore require two pairwise switches to move player 4 into first place in player 1's ranking (one switch between players 3 and 4, and then–once player 4 moves from third place into second place–one switch between players 2 and 4). Likewise, it would require two pairwise switches to move player 1 into first place in player 4's ranking. Altogether, then, four pairwise switches are required to make players 1 and 4 top-ranked choices of each other.

By comparison, it would require only two pairwise switches to make players 3 and 5 top-ranked choices of each other in 2-coalition 35 at level 2. But these are more switches than the zero switches required to make the members of 2-coalitions 12 and 34 top-ranked choices of each other at level 1, because the two players in each of these coalitions are already each other's highest-ranked coalition partners. Accordingly, we have starred coalitions 12 and 34 as the tight 2-coalitions in Example E.

Proposition 5. If preferences are single-peaked, an FB coalition may not be tight.

Proof. In Example E, FB 3-coalition 234 requires three pairwise switches: two to bring players 3 and 4 to the top two ranks in player 2's order; one to bring player 2 to the second rank in player 3's order; and no switches for player 4, which already ranks players 2 and 3 at the top of its order. But 3-coalition 345 requires only two pairwise switches in order to bring player 5 into second place in player 4's order (players 3 and 5 already rank the two other coalition members top in their orders). It is easy to verify that no other 3-coalition in Example E requires as few as two pairwise switches to make its members top-ranked choices in all players' orders, so it is 3-coalition 345, not FB 3-coalition 234, that is tight. Q.E.D.

Proposition 6. If preferences are single-peaked, a disconnected FB coalition may be tight.

Proof. Notice that disconnected FB 4-coalition 1235 in Example D (in the proof of Proposition 3), which requires six pairwise switches, is starred. Connected 4-coalition 1234 also requires six pairwise switches and hence is also tight. But the two other connected 4-coalitions, 2345 and 3456, require seven and eight pairwise switches, respectively, and all disconnected 4-coalitions, except coalition 1235, require eight or more pairwise switches, so coalitions 1235 and 1234 are tied for being the tight 4-coalitions in Example D. Q.E.D.

So far we have shown that FB coalitions may be neither connected (Proposition 3) nor tight (Proposition 5) if preferences are single-peaked. On the other hand, even if an FB coalition is disconnected, which requires a minimum of six players to be uniquely so (Proposition 4), it may still be tight (Proposition 6). FB coalitions have another important property:

Proposition 7. FB coalitions minimize the maximum difference in ranks between coalition members and are, therefore, minimax coalitions.

Proof. Because the descent stops at the level at which, for the first time, a majority of players considers each other mutually acceptable, any earlier stoppage would not produce a majority coalition. Any majority coalition not an FB coalition must have, for some pair of players, greater rank difference. 16 Q.E.D.

In Example E, because FB coalition 234 appears for the first time at level 3, we know there is at least one player (in this case, player 3) that ranks another player in coalition 234 (player 2) as its third-most desirable coalition partner. But coalition 345, which we showed earlier is tight, scores worse on the minimax distance criterion: player 4 ranks player 5 last (i.e., its fourth-most desirable choice), illustrating that a tight coalition may not be minimax.

We have shown that FB (minimax) coalitions may not be tight, and tight coalitions may not be minimax. Assuming they are not the same, as in Example E 17 , we believe FB (minimax) coalitions may be more difficult to disrupt than tight coalitions, because a tight yet non-FB coalition will contain at least one player that is ranked lower by a coalition member than in an FB coalition. This undesired player would seem more likely to be replaced by one or more players closer in rank than in the non-FB coalition, by a coalition partner in an FB coalition may not be tight (because it requires, in toto, more pairwise switches to render its members mutually acceptable and top-ranked choices).

The minimax property of FB coalitions notwithstanding, a different kind of obstacle stands in the way of the formation of FB coalitions:

Proposition 8. FB coalitions may not be minimal majority coalitions (MMCs), whether preferences are single-peaked or spatially single-peaked. 16

Proof. The FB coalition in Example B (single-peaked) and Example C (spatially single-peaked) are the grand coalitions of all four members, not MMCs of three members. Q.E.D.

The MMCs in Example B that are tight are the connected coalitions 123 and 234, which each require one pairwise switch to render their members mutually acceptable and top-ranked choices. These two connected coalitions are also the tight ones in Example C, wherein two pairwise switches are required.

Proposition 9. If preferences are spatially single-peaked, then no FB coalition isdisconnected.

Proof. In section 2, we showed that if preferences are spatially single-peaked, then the clusters of each player's most-preferred coalition partners satisfy a monotonicity property: For any f, i < j implies that g(i) < g(j). This means that as one moves from left to right across the player ordering, then If(i), the set consisting of i's f most-preferred coalition partners, stays the same or moves from left to right also.

Now suppose the i<j<k, and i and k are members of an FB coalition of size f. Then for any member m of the coalition, m must also belong to If(j), because m < g(k) > g(j), and m < h(i) < h(j). Also, j must belong to If(m), because j > i > g(m) and j < k < h(m). It follows that j belongs to the coalition. Q.E.D.

If preferences are single-peaked but not spatially single-peaked, the manipulations in the foregoing proof are not justified. For example, just because i < j < k, it does not necessarily follow that h(i) < h(j) or g(k) > g(j). But if preferences are spatially single-peaked, it is impossible for a disconnected coalition to form under FB. And because it is connected, the FB coalition must include the median player.

5. Quantifying Preferences

So far we have shown that if preferences are single-peaked,

More stringently, if preferences are spatially single-peaked, so players' clusters of preferred coalition partners satisfy the monotonicity property that renders perceptions of distance by all players consistent,

In this section, we drop the assumption that the preferences of players are simply ordinal. Instead, we assume that players can indicate their degrees of preference for coalition partners by expressing, in quantitative terms, how much more they prefer, say, a first-choice coalition partner to a second-choice partner. Thereby we permit players to indicate, cardinally, their intensities of preference.

We continue to identify preference with spatial proximity. For instance, consider Example C, in which the preferences of the players are spatially single-peaked, so the players have a common perception of the ordering of distances between player peaks, which we illustrated earlier as follows:

We can turn this ordinal representation into a cardinal one by making the peaks of the players specific points on the real number line, as illustrated underneath the line below:

Example C'

Now assume that the descent of the players from their peaks does not move, in lockstep, to lower and lower ranks but, rather, that the descent is 0.l units per minute from each peak. 19 Thus, after the elapse of

In our earlier FB ordinal model in section 4, there was a three-step progression from coalitions 12 and 34 (level 1) to 23 (level 2) to the grand coalition 1234 (level 3). In the present cardinal model for the foregoing numerical values, there is a four-step progression from coalition 12 to 34 to 23 to 13 and, thence, to 123, because after 7 minutes all members of coalition 123 become mutually acceptable, which implies MMC 123.

Define the position of a coalition to be the average of the peak positions of its members. In the case of coalition 123, its position is (0 + .2 + .7)/3 = .3.

In all three-person examples, because there are only two different possible orderings for the player in the middle–both of which are consistent with the orderings of the two extreme players–single-peakedness and spatial single-peakedness are equivalent in the FB ordinal model. If player perceptions differ cardinally, however, this model may give very different results from the FB cardinal model.

Proposition 10. FB ordinal and FB cardinal may produce different MMCs with as few as three players.
Proof. Assume the ordinal preferences of the players are as follows:

At level 1, FB ordinal gives coalition 12.

Consistent with these preferences on [0, 1], where player 1 is at 0 and player 3 is at 1, assume player 1 perceives player 2's peak to be at .52, whereas players 2 and 3 perceive player 2's peak to be at .49:

Example F'

Suppose, as earlier, that the players descend from their peaks 0.1 units per minute. Then after 5.1 minutes, players 2 and 3 consider each other mutually acceptable, whereas it would take 5.2 minutes for players 1 and 2 to consider each other mutually acceptable because of player 1's perception of player 2's peak (player 2 would consider player 1 acceptable after only 4.9 minutes). Thus, FB cardinal predicts coalition 23. Q.E.D.
Proposition 11. If preferences are single-peaked, an FB cardinal coalition can be disconnected if there are five, but not fewer, players. 20
Proof.Associate with each player's ordinal ranking in Example E the following cardinal values (in the case of player 2's perception of player 3's position, assume it is .20 + to ensure that player 2 prefers player 1 to player 3–as assumed in the rankings of Example E–but suppose is sufficiently small that, for calculational purposes, .20 can be used):

After 3 minutes, players 1, 2, and 4 all consider each other mutually acceptable–and will also consider player 3 acceptable as a coalition partner–as shown by the brackets that extend from these players (in boldface) by .3 units to either side, unless stopped at the left boundary of 0. However, player 3 does not share this perception and desires, instead, to be in a coalition with players 4 and 5 after only 2 minutes. More extreme, player 5 does not desire any coalition partner after an elapse of 3 minutes, or even up to 7 minutes.

Consequently, the first FB cardinal coalition to form, based on the cardinal values of this example, will be disconnected coalition 124. It will be located at position (0 + .1 + .3)/3 = .133 on all players' cardinal scales except player 3's, where it will be at position (0 + .1 + .9)/3 = .333.

Such a disconnected coalition cannot form if there are only three or four players, because a disconnected coalition would have to include both endpoints. Consequently, the grand coalition would form at the same time as all smaller majority coalitions, so a disconnected majority coalition cannot form under the FB cardinal model with only four or fewer players. Q.E.D.

Thus, our FB cardinal model reduces the minimal example of a unique disconnected coalition from six players in the ordinal model to five in the cardinal model. Again, the key to the formation of a disconnected FB cardinal coalition is that the preferences of the players not be spatially single-peaked. 21 But preferences might be almost spatially single-peaked, as Example E' demonstrates, and the paradox still occur: Except for player 5, all players associate exactly the same cardinal values with each others' positions (with the minor exception of player 2's believing player 3 is at .20 + rather than .20). Translated back into ordinal terms, all players except player 3 think the biggest gap is between players 4 and 5, whereas player 3 thinks the biggest gap is between itself and player 4.

6. Build-Up (Constrained) Coalition Formation

Having shown how an FB cardinal model may reduce the minimum number of players necessary to produce a unique disconnected majority coalition from six to five, we now turn to a new model of coalition formation, called build-up coalition formation (BU), wherein cardinal preferences, because of the averaging of the positions of composite players in the model, play a central role, so no ordinal model will be presented. BU proceeds as follows:

  1. The descent is the same as under the FB cardinal model except that, once a subcoalition forms (i.e., when two or more players become mutually acceptable), this subcoalition becomes a composite player, whose peak is located at the weighted average of the peak of its component players.
  2. Each time a composite player forms, the descent begins anew in the new and smaller "game," comprising both individual and composite players, until a majority coalition forms for the first time. The process stops, with the resulting largest majority coalition(s) designated BU coalition(s).

We illustrate BU with Example C':

Example C'

The first subcoalition to form is 12, which becomes a composite player at .1:
The next subcoalition to form is 34, which becomes a composite player at .85:
Finally, the grand coalition, 1234, will form at position (.10 + .85)/2 = .475 22 , which becomes the BU coalition, compared with the FB cardinal prediction of MMC 123 at position .3.

Coalition formation is constrained in the BU model, compared to the FB cardinal model, because the players in each subcoalition that forms, now fused into a single player, cannot be selectively excluded from any future majority coalition. In particular, player 4, left out when MMC 123 forms in the FB cardinal model, must be included in the BU model–once subcoalition 34 forms–so it is the grand coalition, 1234, that forms in Example C' under BU.

What BU coalition will form in our 5-person cardinal example of the paradox of disconnected coalitions (see Example E' in section 5) is more complicated to determine because preferences are not spatially single-peaked. Because all players perceive the distance separating players 1 and 2, and 3 and 4, to be 0.1 unit, subcoalitions 12 and 34 will form at the positions shown below after 1 minute:

Example E'

After the elapse of another 7.5 minutes (because the greatest distance separating players 34 and 5 is .75 units, which is less than the greatest distance of .80 units separating players 12 and 34), 23 BU connected coalition 345 will form, which differs radically from disconnected coalition 124 that the FB cardinal model produced. The position of MMC 345, reflecting the fact that subcoalition 34 has twice the weight of player 5, will be at .50 in the perception of players 1, 2, 4, and 5, and at .90 in the perception of player 3 (for FB cardinal coalition 124, it will be recalled, these positions were decidedly to the left at, respectively, .133 and .333).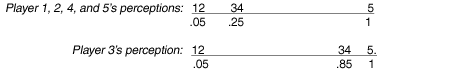

In effect, the conjoining of players 3 and 4 at the beginning precludes coalition 124, even though players 1, 2, and 4 are all within 0.3 units of each other. Thereby the formation of subcoalitions under BU can put severe constraints on what later majority coalition forms, and its position for the different players.

One might think that such constraints would prevent the formation of disconnected coalitions, but this is not the case:

Proposition 12. If preferences are single-peaked, a BU coalition can be disconnected if there are as few as five players. 24
Proof. Modify Example E' so that the perceptions of players 1, 2, 4, and 5 do not change but player 3's perception does:
Example E''
After the elapse of 1 minute under BU, we obtain:
After the elapse of another 2.5 minutes (because, for players 1, 2, and 4, the distance separating composite player 12 and player 4 is .25 units), BU disconnected coalition 124 will form at position [2(.05) + .3]/3 = .133 for players 1, 2, 4, and 5, and position [2(.05) + .9]/3 = .333 for player 3. Q.E.D.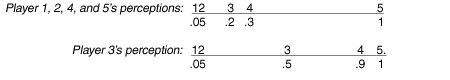

Disconnected coalition 124 at the foregoing positions is also the prediction of the FB cardinal model for Example E'' after 3 minutes, which is the time it takes for players 1 and 4, and therefore player 2 between them, to find each other mutually acceptable. The "problem" for player 3 under both models is that whereas players 1, 2, and 4 consider player 3 to be acceptable after the elapse of 3 minutes in the FB cardinal model and 3.5 minutes in the BU model, player 3 does not deem them acceptable because it is too far away, on both the left and the right, from them. To be sure, player 5 is even farther from all players–except as player 3 perceives the situation–so player 5 will suffer the most when MMC 124 forms at position .133.

While the BU model may tend to produce larger majority coalitions than the FB cardinal model, Example E'' demonstrates that BU may, nevertheless, produce MMCs, and disconnected ones at that, if preferences are single-peaked. Nevertheless, the FB cardinal model fares better than the BU model in terms of two measures of closeness.

Define a majority coalition to be cardinally minimax if it minimizes the maximum cardinal distance between adjacent pairs of players; it is cardinally tight if the cardinal distance between its most extreme members (i.e., on the left and right) is minimal among all majority coalitions.

Proposition 13. If preferences are spatially single-peaked, FB cardinal coalitions are connected, cardinally tight, but may not be cardinally minimax 25 .

Proof. Because dij = dji , player i finds player j acceptable as a coalition partner exactly when j finds i acceptable. At that instant, players i and j, and all players in between them, form an FB cardinal coalition. Thus, any FB cardinal coalition is connected. Moreover, the first majority coalition to form must be the one that minimizes the distance between its extreme members, so the FB cardinal coalition is cardinally tight.

That this coalition need not be cardinally minimax is illustrated by a 5-player example whose player positions are (0, .1, .49, .7, 1). The first majority coalition to form under FB cardinal will be that comprising the first three players (123), for which the maximum distance between adjacent players is .39 (.49 - .1). But there is another majority coalition, 345, for which the maximum distance between adjacent players is .30 (1 - .7), so it is the latter coalition that is cardinally minimax. Q.E.D.

Proposition 14. If preferences are spatially single-peaked, a BU coalition may be neither cardinally minimax nor cardinally tight.
Proof.Consider the following 5-person example:
Example G
The first subcoalition to form under BU is 34, which becomes a composite player at position .62: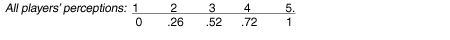
The next subcoalition to form is 12, which becomes a composite player at position .13: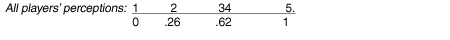
Finally, BU coalition 345 will form at position [2(.62) + 1]/3 = .75: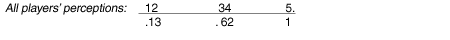
The maximum cardinal distance between adjacent pairs of players in coalition 345 is .28 between players 4 and 5, and the cardinal distance separating its extreme members (players 3 and 5) is .48. These distances are both greater than those of FB coalition 234: The maximum distance between adjacent pairs of members (players 2 and 3) is .26, and the cardinal distance separating its extreme members (players 2 and 4) is .46. Q.E.D.

We remarked in section 5 that if preferences are spatially single-peaked, FB cardinal coalitions will be connected for essentially the same reasons, as given in Proposition 9, that FB ordinal coalitions are. This reasoning can be extended to BU coalitions:

Proposition 15. If preferences are spatially single-peaked, BU coalitions are always connected.
Proof. The first subcoalition to form under BU comprises the closest pair of players, which must be adjacent (otherwise, there would be a closer pair); the first subcoalition is therefore connected. At any stage, the next subcoalition to form must join the two closest players at that stage. Again, these players, which may be either individual or composite, must be adjacent. If all coalitions formed prior to this stage are connected, then the new subcoalition must also be connected. Thus, at any stage, any coalition that forms under BU is connected. Q.E.D.

In the final section, we will compare our ordinal and cardinal models and offer some conclusions about their applicability to coalition formation in such institutions as parliaments. We will also propose an extension of the models that is suggested by the alliances that formed, and the reasons that motivated their members to coalesce, during World Wars I and II.

7. Conclusions and Extensions

Instability plagues many n-person situations in which players seek to form majority coalitions. Even when their preferences for coalition partners are spatially single-peaked, players may still have an incentive to defect.

In the face of such instability, we proposed two coalition-formation models that describe how coalitions might plausibly form. The models share the assumption that players coalesce when they find each other mutually acceptable.

In the ordinal version of the fallback (FB) model, players seek coalition partners by descending lower and lower in their preference rankings until a majority coalition emerges. In the cardinal version, players move at a uniform rate away from their peaks along a continuous dimension.

Subcoalitions that form early do not restrict future choices, suggesting FB as a model of unconstrained coalition formation. Because players can abandon early subcoalition partners in order to be part of the first majority coalition to form later, they may be thought of as acting nonmyopically.

In the build-up (BU) model, by comparison, the subcoalitions fuse into composite players, with the descent recurring each time a new composite player forms. Because these composite players cannot be broken apart, their formation may impede the build-up of coalitions that otherwise would form.

Thereby the growth of coalitions is constrained under BU. It is also myopic in the sense that the "baggage" of coalition partners that players pick up early, when subcoalitions form that may hurt them later, cannot be detached. Because the positions of composite players are based on weighted averages, BU is developed only as a cardinal model, making it more comparable to the cardinal than the ordinal version of FB.

We summarize our main results. If preferences are single-peaked,

If preferences are spatially single-peaked,

Thus, while single-peakedness is not sufficient to prevent disconnected coalitions from forming, the stronger condition of spatial single-peakedness–which presumes that players have similar, if not identical, perceptions of the distances separating themselves along the dimension–is sufficient. But even if preferences are spatially single-peaked, BU coalitions need be neither cardinally minimax nor cardinally tight, though FB ensures the latter property.

In legislatures, the myopia of BU is probably more prevalent than the nonmyopia of FB in the passage of ordinary legislation. Typically, small groups of members coalesce before trying to put together a larger winning coalition. Rarely do these groups split apart, once they form, as they gather strength by enlisting new members. 26

On the other hand, when a political party is asked to form a new government in a parliamentary democracy, FB may be a better mirror of the manner in which the governing coalition emerges. The party's leaders weigh simultaneously different combinations of other parties to try to find the set of coalition partners that it can best work with to advance its legislative program. Because party leaders must think beyond the next piece of legislation they want enacted, their thinking is more likely to be farsighted than that of ordinary legislators struggling to win on the next vote.

Whether it is individual legislation or parliamentary control that is sought, the old saw that "politics makes strange bedfellows" is often observed. However, while FB or BU might be the main engine that drives the coalition-formation process, we think there is often another significant factor that helps to explain why some coalitions rather than others form: a wary concern that the opposition might gain an unbeatable edge unless one strikes a deal rapidly, speeding up coalition formation among unlikely partners. 27

To illustrate this situation at the start of World War I, after the assassination of Archduke Franz Ferdinand of Austria-Hungary by a Serbian nationalist in June 1914, Austria issued an unacceptable ultimatum to Serbia, causing Russia to throw its support to Serbia and commence secret military preparations. Learning of these, German Kaiser Wilhelm II wrote on the margin of a message he had received from Russian Czar Nicholas II: "And these measures are for a defense against Austria, which is in no way attacking him [Russia]!!!" Incredulous that the Czar would see the much smaller Austria as a threat to Russian security, the Kaiser concluded that Russia's mobilization was really aimed against Germany, and he responded accordingly: "Begin [preparations]! Now!" (quoted in Holsti, 1965: 368). Clearly, player perceptions fed on each other. 28

But the spiraling conflict that created World War I did not stop there. As Germany rushed to support Austria-Hungary, France threw its weight behind Russia, and Britain intervened to help France after Germany violated Belgium's neutrality. Montenegro and Japan soon joined the Allies, as did Italy in May 1915; the Ottoman Empire sided with the Central Powers and later was joined by Bulgaria in October 1915. In 1916, Portugal and Romania were drawn into the maelstrom on the side of the Allies, as was the United States in 1917, after which Russia withdrew from the war following its October revolution. As the models prescribe, both sides tried to achieve winning status by progressively enlisting alliance partners who were originally less acceptable or more reluctant to join.

In World War II, military alliances were also fueled by perceptions of what the potential opposition might do. But in this war, there were certainly more "unholy alliances," as when fascist Germany, to neutralize opposition on its eastern front, made a nonaggression pact with communist Soviet Union in August 1939 (it violated it less than two years later when Hitler invaded the Soviet Union in June 1941). When Japan wound up an ally of Germany–a country pledged to make Aryans the controlling race–after the Japanese attack on Pearl Harbor in 1941, the Axis gained another strange bedfellow.

The formation of disconnected coalitions like these, we believe, is facilitated not just by mutual desires but also by mutual antipathies, and concomitant fears of losing if one does not make quick deals with players that might otherwise join the opposition. It is unclear how best to bring such calculations into the FB and BU models, but we think that the dread of losing, should one not act quickly enough to consolidate one's position, is frequently a major force behind coalition formation.

It is worth reiterating our main finding: Closeness calculations, paradoxically, may be the driving force behind disconnected coalitions when preferences are single-peaked–though not when they are spatially single-peaked. If different perceptions of closeness create unholy alliances, the nonmyopic FB model will tend to produce smaller coalitions, the myopic BU model larger ones. 29

 

Bibliography

Axelrod, Robert (1970). Conflict of Interest: A Theory of Divergent Goals with Applications to Politics. Chicago: Markham.

Brams, Steven J., and D. Marc Kilgour (1999). "Fallback Bargaining." Preprint, Department of Politics, New York University.

Brams, Steven J., and D. Marc Kilgour (1988). Game Theory and National Security. New York: Basil Blackwell.

Brams, Steven J., and Alan D. Taylor (1996). Fair Division: From Cake-Cutting to Dispute Resolution. New York: Cambridge University Press.

Bronner, Ethan (1999). "Left and Right Are Crossing Paths." New York Times, July 11, section 4, pp. 1, 5.

Bueno de Mesquita, Bruce (1981). The War Trap. New Haven, CT: Yale University Press.

Bueno de Mesquita, Bruce, and David Lalman (1992). War and Reason. New Haven, CT: Yale University Press.

Chakravorti, Bhaskar (1999). "Far-Sightedness and the Voting Paradox." Journal of Economic Theory 84, no. 2 (February 1999): 216-226.

Coombs, Clyde H. (1964). A Theory of Data. New York: John Wiley and Sons.

Demange, Gabrielle (1994). "Intermediate Preferences and Stable Coalition Structures." Journal of Mathematical Economics 23: 45-58.

DeSwaan, Abraham (1970). "An Empirical Model of Coalition Formation as an N-Person Game of Policy Minimization." In Sven Groennings, E. W. Kelley, and Michael Leiserson (eds.), The Study of Coalition Behavior: Theoretical Perspectives and Cases from Four Continents. New York: Holt, Rinehart and Winston, pp. 424-444.

DeSwaan, Abraham (1973). Coalition Theories and Cabinet Formation. Amsterdam: Elsevier.

de Vries, Miranda W. M. (1999). Governing with Your Closest Neighbour: An Assessment of Spatial Coalition Formation Theories. Ph.D. dissertation, Catholic University of Nijmegen, The Netherlands.

Downs, George W., David M. Rocke, and Peter H. Barsoom (1998). "Managing the Evolution of Multilateralism." International Organization 52, no. 2 (Spring): 397-419.

Epstein, Joshua M. (1999). "Agent-Based Computational Models and Generative Social Science." Complexity 4, no. 5 (May/June): 41-60.

Garrett, Geoffrey, and George Tsebelis (1999). "Why Resist the Temptation to Apply Power Indices to the European Union?" Journal of Theoretical Politics 11: 291- 308.

Grayson, George W. (1999). Strange Bedfellows: NATO Marches East. Lanham, MD: University Press of America.

Greenberg, Joseph, and Shlomo Weber (1986). "Strong Tiebout Equilibrium under Restricted Preferences Domain." Journal of Economic Theory 38: 101-117.

Greenberg, Joseph, and Shlomo Weber (1993). "Stable Coalition Structures with a Unidimensional Set of Alternatives." Journal of Economic Theory 60: 62-82.

Grofman, Bernard (1982). "A Dynamic Model of Protocoalition Formation in Ideological N-Space." Behavioral Science 27: 77-99.

Grofman, Bernard (1996). "Extending a Dynamic Model of Protocoalition Formation." In Norman Schofield (ed.), Collective Decision-Making: Social Choice and Political Economy. Boston: Kluwer Academic, pp. 265-280.

Grofman, Bernard, Philip Straffin, and Nicholas Noviello (1996). "The Sequential Dynamics of Cabinet Formation, Stochastic Error, and a Test of Competing Models." In Norman Schofield (ed.), Collective Decision-Making: Social Choice and Political Economy. Boston: Kluwer Academic, pp. 281-293.

Hinich, Melvin J., and Michael C. Munger (1997). Analytical Politics. New York: Cambridge University Press.

Holsti, Ole R. (1965). "The 1914 Case." American Political Science Review 59: 365-378.

Levy, Jack S. (1990/91). "Preferences, Constraints, and Choices in July 1914." International Security 15: 151-186.

Levy, Jack, Thomas J. Christensen, and Marc Trachtenberg (1991). "Correspondence: Mobilization and Inadvertence in the July Crisis." International Security 26: 189-203.

Maoz, Zeev (1990). Paradoxes of War: On the Art of National Self-Entrapment. Boston: Unwin Hyman.

Merrill, Samuel III, and Bernard Grofman (1999). A Unified Theory of Voting: Directional and Proximity Spatial Models. New York: Cambridge University Press.

Robertson, Jack, and William Webb (1998). Cake-Cutting Algorithms: Be Fair if You Can. Natick, MA: A K Peters.

Shepsle, Kenneth A., and Mark S. Bonchek (1997). Analyzing Politics: Rationality, Behavior, and Institutions. New York: W. W. Norton.

Straffin, Philip D. Jr., and Bernard Grofman (1984). "Parliamentary Coalitions: A Tour of Models." Mathematics Magazine 57, no. 5 (November): 259-274.

Tiebout, Charles M. (1956). "A Pure Theory of Local Expenditures. Journal of Political Economy 64: 416-424.

Trachtenberg, Marc (1990/91). "The Meaning of Mobilization in 1914." International Security 15: 120-150.

Van Deemen, Ad M. A. (1997). Coalition Formation and Social Choice. Dordrecht, The Netherlands: Kluwer Academic.

Zagare, Frank C., and D. Marc Kilgour (2000). Perfect Deterrence. Cambridge, UK: Cambridge University Press (forthcoming).

Endnotes

*: Department of Politics New York University; New York, NY 10003; UNITED STATES; steven.brams@nyu.edu Back.

**: Department of Mathematical Sciences Montclair State University; Upper Montclair, NJ 07043; UNITED STATES; jonesma@pegasus.montclair.edu Back.

***: Department of Mathematics Wilfrid Laurier University; Waterloo, Ontario N2L 3C5; CANADA; mkilgour@wlu.ca Back.

Note 1: Steven J. Brams gratefully acknowledges the support of the C. V. Starr Center for Applied Economics at New York University, and D. Marc Kilgour the support of the Social Sciences and Humanities Research Council of Canada. We thank Peter C. Fishburn, Bernard Grofman, and William S. Zwicker for valuable comments and discussions. Back.

Note 2: There is nothing sacrosanct about stopping the process at a simple majority; the stopping point could be any qualified majority, up to and including unanimity. To avoid strategic problems that could arise about the order of players' joining a coalition if players are unequally weighted, we focus on situations in which the players are equally weighted. Back.

Note 3: Garrett and Tsebelis (1999: 294) declare such a coalition "impossible," but they offer no model of coalition formation to explain why this is the case except to say that an "excluded member [from an otherwise connected coalition] will go along." We will show why this need not be the case. The literature on spatial models, particularly of voting, is vast, but good overviews can be found in Hinich and Munger (1997) and Shepsle and Bonchek (1997). An excellent synthesis that unifies the so-called directional and proximity spatial models is given in Merrill and Grofman (1999). Back.

Note 4: To demonstrate formally that the players order the distances differently in Example B, and hence their preferences cannot be described by a single spatial model, note that player 2's ranking implies d 34 < d 24 < d 12, whereas player 3's ranking implies d 12 < d 13 < d 34. This contradiction shows that player preferences in Example B, while single-peaked with respect to the ordering 1-2-3-4, are not spatially single-peaked. Back.

Note 5: To prove this statement, fix f and suppose that j > i. If j > h(i), the statement holds because g(j) > j - f + 1 > h(i) - f + 1 = g(i). Otherwise, i < j < h(i). Suppose that k < g(i). Because k < i < j, d kj > d ki . Because h(i) is among i's f most-preferred coalition partners, and k is not, it must be the case the d ki > d i,h(i) > d j,h(i) . Therefore, d kj > d j,h(i) . Now assume (to obtain a contradiction) that k is among j's f most-preferred coalition partners. Then so is h(i), because d kj > d ki > d j,h(i) . But this is impossible, because j's f most-preferred coalition partners form an "interval," {g(j), g(j) + 1, . . . , h(j)}, where h(j) - g(j) = f - 1. But h(i) - k > h(i) - g(i) = f - 1, demonstrating that both h(i) and k cannot both belong to an interval containing f players. This contradiction shows that if k < g(i), then k < g(j), completing the proof that g(i) < g(j). Back.

Note 6: Demange's (1994) notion of "intermediate preferences" also satisfies this monotonicity property. Whereas Demange gives conditions under which intermediate preferences lead to stable connected coalitions in a cooperative game-theoretic model, we show in section 3 that there may be no stable coalitions, in a noncooperative sense, even when preferences are spatially single-peaked. When they are not, disconnected coalitions also may form. Back.

Note 7: After completing an earlier version of this paper, we were alerted by Peter C. Fishburn to the "unfolding" technique of Coombs (1964) for determining whether stimuli and other kinds of psychological data can be represented by unidimensional and multidimensional scales. In the unidimensional case, individual preferences (I scales) are single-peaked if they can be "unfolded" into a qualitative J ("joint") scale, and spatially single-peaked if they can be unfolded into a quantitative J scale. Whereas Coombs' interest was in constructing J scales–qualitative or quantitative–from a set of I scales, ours is in determining whether a qualitative J scale (single-peaked preferences) is also a quantitative J scale (spatially single-peaked). Among other things, Coombs noted that as the number of players increases, the proportion of single-peaked preferences that are spatially single-peaked tends to zero, making the paradox discussed here increasingly likely. Back.

Note 8: Note that our definition of "instability" does not presume there exists a stable two-person coalition; in fact, in this example there does not, as we will show next. Surprisingly, such instability also characterizes situations in which majority preferences are transitive (i.e., do not lead to cyclical majorities), as we will illustrate with Examples B and C. If, unlike Examples A, B, and C, no player desires to switch to another majority coalition, there is a so-called Tiebout equilibrium (Tiebout, 1956; Greenberg and Weber, 1986, 1993; Demange, 1994). It is worth noting here, however, that our analysis is not game-theoretic: We do not define a game and analyze its equilibria but instead postulate coalition-formation processes that seem likely to support, if not stabilize, the coalitions that do form. In doing so, we focus on the preferences of players for each other, and indirectly on coalitions that are aggregations of preferred players. Thus, we do not analyze the policies that the coalitions can enact, and the associated payoffs of players for these policies, in a game. For good reviews, with empirical examples, of game-theroetic models of coalition formation applicable to cabinet formation in parliamentary systems, see van Deemen (1997) and de Vries (1999). Back.

Note 9: When there are four players, single-peakedness implies that players 1 and 4 must rank the other players exactly according to the dimensional ordering, going from left to right and from right to left, respectively. Player 2 may rank either adjacent player 1 or adjacent player 3 first–and if player 3, either player 1 or player 4 next. Player 3 may rank either adjacent player 2 or adjacent player 4 first–and if player 2, either player 1 or player 4 next. Only one of these nine possible orderings for players 2 and 3, which is Example B, is single-peaked without also being spatially single-peaked. Back.

Note 10: As illustrated in the text, there must be a bigger gap between positions 2 and 3 than between positions 1 and 2 (because of player 2) and between positions 3 and 4 (because of player 3). Between positions 1 and 2 and positions 3 and 4, however, the preferences in Example C do not imply an ordering, which makes the players' commonly perceived ordering incomplete, whereas in our visual representation in the text, d 34 is shown to be greater than d 12. This representation demonstrates that there is a single spatial model consistent with all players' preferences, establishing that the players' preferences are spatially single-peaked. But this illustration is just one possible example; if x 1 = 0 and x 4 = 1, then the ordering of Example C is achieved by any spatial model in which the point (x2, x3), representing the locations of players 2 and 3, satisfies (1/2)(1 + x 2) < x 3 < 1 and 0 < x 2 < x 3/2. For example, these inequalities are satisfied whenever x 2 [0, 1/3) and x 3 (2/3, 1]. Back.

Note 11: Stronger conditions that do ensure stability have been proposed in, among other places, Greenberg and Weber (1986, 1993) and Demange (1994). We do not, as we shall explain next, pursue this search for sufficient conditions but instead focus on processes by which coalitions grow. The latter approach is more algorithmic than axiomatic in the sense that it postulates rules for players' combining, rather than postulating conditions that would render the resulting combinations equilibria in a game-theoretic sense. This "generative" approach to deriving macroscopic behavior from microscopic assumptions is espoused in, among other places, Epstein (1999). Back.

Note 12: If there were an odd number of players and preferences did not cycle (unlike Example A), there would be a Condorcet player, whose peak is at the median and who could defeat all other players in pairwise contests. Back.

Note 13: To see this, note that player 4's ranking implies d56 < d46 < d34 , and player 5's ranking implies d34 < d35 < d56 , which are inconsistent. Back.

Note 14: This is why we do not include coalitions 13 and 23 at level 2, and coalitions 15, 25, 35, 125, 135, and 235 at level 4, in our listing of coalitions in the text: they are, respectively, proper subsets of coalition 123 at level 2, and coalition 1235 at level 4. Back.

Note 15: Like Example D (see note 12), the players' preferences in Example E are single-peaked but not spatially single-peaked: Player 3's ranking implies d 45 < d 35 < d 23, and player 4's ranking implies d 23 < d 24 < d 45, which are inconsistent. Back.

Note 16: Unlike our earlier propositions, note that this argument holds for any preferences, not just those that are single-peaked or spatially single-peaked. Back.

Note 17: In Example D, by contrast, one of the tight coalitions, 1235, is also an FB (minimax) coalition, as shown in the proof of Proposition 6. Back.

Note 18: As indicated in note 2, while all majority coalitions are simple-majority coalitions, they could as well be qualified-majority coalitions. Back.

Note 19: This is analogous to a knife moving across a cake in the fair-division literature (Brams and Taylor, 1996; Robertson and Webb, 1998), except that in our coalition-formation model, no player calls "stop" to halt the knife; instead, the process stops, automatically, when a majority coalition forms for the first time. Back.

Note 20: We assume that all player perceive the distance between extremes to be the same or, equivalently, that all players' "acceptability regions" grow at a constant rate, proportional to the perceived gaps between the extremes. Otherwise, disconnected coalitions could form with as few as three players. Back.

Note 21: The reasoning is analogous to that given in the proof of Proposition 9–but now with the players' cardinal ratings substituting for ordinal rankings–so it will not be given here. In the cardinal model, however, we take spatial single-peakedness to mean that the players have exactly the same perceptions of each others' positions on the left-right dimension–not just that there is no inconsistency in their orderings–in which case player i finds player j desirable if and only if j finds i acceptable. It follows immediately that a player situated between i and j must be included in a coalition that contains them, thereby precluding disconnected coalitions. Back.

Note 22: Here simple averaging of the positions of individual players, and of the pairs that combine is possible, but later we will need to do weighted averaging to determine the positions of players, and subcoalitions of different size, that combine. The successive use of weighted averaging to determine the position of any BU coalition is equivalent to the simple averaging of the positions of all its individual members. Back.

Note 23: Alternatively, we could assume that player 5 does not return to its to original extreme position of 1 after 1 minute but instead has moved to a new position at .9. In this case, the emergence of coalition 345 would take an additional 6.5 rather than 7.5 minutes. This alternative calculation of elapsed time until a coalition forms has no effect on our subsequent results on what coalitions emerge–only when they do so–and their positions. Back.

Note 24: In a dynamic model of coalition formation that somewhat resembles our BU model, Grofman (1982) and Straffin and Grofman (1984) show that coalitions will always be connected in one dimension but not necessarily in two or more dimensions (i.e., all players in the convex hull defined by the spatial positions of coalition members may not be in the coalition, creating "holes" in space rather than along a line); for extensions of this model, and applications to coalition-formation data in different European parliamentary democracies, see Grofman (1996) and Grofman, Straffin, and Noviello (1996). In our BU model, connectedness obtains in one dimension, as we will show shortly (Proposition 15), if preferences are spatially single-peaked, which Grofman and his coauthors implicitly assume. On the other hand, if preferences are single-peaked without being spatially single-peaked, coalitions may be disconnected, as we next prove. Back.

Note 25: The fact that BU coalitions may not be cardinally tight shows that DeSwann's (1970, 1973) assumption of "policy distance minimizing" coalitions may not hold, even when preferences are spatially single-peaked. Whereas spatially single-peaked preferences are sufficient to ensure connected coalitions (Proposition 15), Axelrod's (1970) assumption of unidimensinally connected coalitions is inconsistent with preferences that are single-peaked but not spatially single-peaked, whether the coalition-formation model is FB, FB cardinal, or BU. The fact that the assumptions of the DeSwann and Axelrod run amok of some of our results should not detract from the fact that these models have proved quite accurate descriptively, at least in predicting parliamentary coalitions. Our models, while less intended to explicate outcomes than the processes by which they are engendered, do, nevertheless, pinpoint conditions under which disconnected and nontight coalitions, though perhaps exceptional, are likely to form (see section 7 for examples). Back.

Note 26: This sequential build-up strategy is what Downs, Rocke, and Barsoom (1998) argue contributes to the depth of cooperation among members of a multilateral organization. Back.

Note 27: We make no attempt here to test this notion on, or apply the FB and BU models to, the build-up of legislative coalitions or the formation of governments in parliamentary democracies. In lieu of systematic testing with such data, which we plan to do in the future, we next offer brief illustrations of coalition formation in a different realm. Back.

Note 28: Several analysts contend, without invoking the kinds of coalition models developed herein, that World War I was more a product of deliberate calculations than a loss of control over events, especially during the escalating crisis in July 1914; see Trachtenberg (1990/91), Levy (1990/1991), and Levy, Christensen, and Trachtenberg (1991). More general arguments that wars are not inadvertent but the result of rational calculations can be found in, among other places, Bueno de Mesquita (1981), Brams and Kilgour (1988), Maoz (1990), Bueno de Mesquita and Lalman (1992), and Zagare and Kilgour (2000). Back.

Note 29: Bronner (1999) gives many contemporary examples. As argued here, it may not be just that the left and right, in Bronner's terms, are "crossing paths," or that there is no longer a left-right spectrum, but that perceptions of distance along this ordering are more divergent than ever before. Grayson (1999) argues that NATO, recently expanded to include former communist states, now embraces strange bedfellows (which is, in fact, the title of his book). Back.