|
|
|
|
Tripolarity and Hitler’s Strategy of World Conquest
1998
2. A Study of Tripolar Systems
Discussions of polarity in international relations theory generally focus on the distinction between bipolar and multipolar systems. Tripolar systems are either ignored or lumped under the broader rubric of multipolarity. This chapter asks the question, Does tripolarity merit study apart from other systems of greater and lesser numbers of poles? To answer this question, we must first determine what distinguishes one type of international system from another.
Why Study Tripolarity?
Typically, but by no means exclusively, international systems have been demarcated by their differing polarities. 1 The term polarity usually refers to the number of Great Powers in the system. Given the sloppy state of the conceptual analysis in the field of international relations, however, polarity is frequently (mis)used in a behavioral rather than a purely structural sense to connote the number of antagonistic blocs in the system. 2 The problem with the latter definition is that it conflates the distinct concepts of polarity (the number of poles) and polarization (the number of alignments in the system).
In terms of the properties exhibited by the system, however, the addition of one Great Power, or pole, to any given power distribution does not always represent a meaningful change in system polarity. For instance, it is generally agreed that a new system occurs when moving from one to two poles or from two to three poles but not when moving from, for example, seven to eight poles or fifty to fifty–one poles. This means that in addition to knowing how systems are classified (i.e., what elements define the system under observation), we need to know what kinds of change constitute system transformation (a change in its dynamics) as opposed to changes within the system.
The key issue is whether a change in the defining properties (i.e., in structural realist theory, an additional pole) alters the dynamics of the system. In reference to the prior examples, we distinguish between systems of two and three poles because two is postulated to be a threshold for the specific characteristics exhibited by that system; while in the latter two examples, seven and fifty are not generally considered thresholds for their respective system dynamics.
Returning to our initial question, Is three a threshold number of poles? Since there is no debate that bipolar systems behave differently than systems of greater than two actors, it is a question of whether to distinguish between systems of three poles and those of four or more poles. Most theorists agree that three is indeed a threshold number. Robert Gilpin says, “Although students of international relations disagree on the relative stability of bipolar systems versus multipolar systems, almost all agree that a tripolar system is the most unstable configuration.” 3 Likewise, Morton Kaplan and Kenneth Waltz associate tripolarity with extreme systemic instability. Kaplan asserts, “If there are only three essential national actors and if they are relatively equal in capability, the probability that two will combine to eliminate the third is relatively great.” 4 Likewise, Waltz argues that “systems of three have distinctive and unfortunate characteristics. Two of the powers can easily gang up on the third, divide the spoils, and drive the system back to bipolarity. In multipolar systems four is then the lowest acceptable number [for balancing to occur], for it permits external alignment and promises considerable stability.” 5
Conversely, some theorists claim that tripolarity is the most stable system. In their study of system polarity and the frequency of major wars, Charles Ostrom and John Aldrich find tripolarity to be the most peaceful power configuration. 6 Likewise, David Garnham posits “a curvilinear relationship between the number of poles in the interstate system and the probability of major power war. The likelihood of war is lowest for a tripolar system, higher for a bipolar system, highest in a system with five poles, and less likely in larger systems. 7
Much of the confusion about the stability of tripolar systems arises because some analysts (e.g., Waltz and Kaplan) define tripolarity as a system composed of three actors of roughly equal size, while others (e.g., Ostrom and Aldrich) identify tripolarity with any triadic configuration, regardless of the size disparities among the three units. Additional confusion arises because, as previously mentioned, some analysts use a behavioral definition (polarization) rather than a structural definition of system polarity. For such analysts, any conflict between two sides is bipolar, between three sides, tripolar, etc., no matter how many individual members are involved.
In addition, the two contradictory views of tripolarity can be partially explained by the unique ambiguity of coalitions in triads. Sometimes, the third member can act as a mediator or balancer; other times as an instigator or kingmaker. In the following passage, Georg Simmel notes this peculiar property:
| Where three elements, A, B, C, constitute a community, there is added to the immediate relationship which exists, for example, between A and B, the immediate relationship which they gain by their common relation to C. . . Separations which the parties could not of themselves reconcile are accommodated by the third, or by their being included in a comprehensive whole. On the other hand, the direct union is not merely strengthened by the indirect, but it may also be destroyed. There is no relationship so complete between three that each individual may not, under certain circumstances, be regarded by the other two as an intruder. . . 8 |
As Simmel suggests, within a given tripolar system, the types of coalitions that form and the degree of stability exhibited is a function not only of the distribution of capabilities within the triad but also of the identity and interests of the units, that is, the relationships that form among the three members.
Tripolarity and System Stability
Why are tripolar configurations believed to be so unstable? Consider the effect of polarity on balance&-;of–power systems composed of all equally sized units (a simplifying assumption that will be relaxed in the later discussion of tripolar dynamics). In addition, assume that all states must choose one side or the other—none can be neutral. For descriptive purposes, I will invoke the well–worn “image of two scales suspended upon a fulcrum, balancing only when equal weights are placed upon the two scales.” 9 It is immediately obvious that all even–numbered systems are capable of balance, while all odd–numbered systems are not. This alone distinguishes a tripolar from a quadrapolar system. But how does this distinguish tripolarity from other odd–numbered systems? Coalition formation in the tripolar system will tilt the scale far more out of balance than it would any other odd–numbered system. In other words, when an odd–numbered system devolves into two opposing alliances, the inequality between the larger and smaller coalitions is greatest in a tripolar system, where one side is twice as strong as the other.
The equation to reflect the amount of inequality in the resources held by the stronger and weaker coalitions is: I = ([a – b]/b) x 100, where a = the resources of the larger coalition, b = the resources of the smaller coalition, p = the polarity of the system. The difference between the two coalitions is treated as a percentage of the amount held by the weaker coalition. Thus for p = 3: I = ([66 – 33]/33) x 100 = 1 x 100, or there is a 100 percent difference in strength between the stronger and weaker coalitions in a tripolar system. For p = 5: I = ([60 – 40]/40) x 100 = .5 x 100, or 50 percent. For p = 7: I = ([57 – 43]/43) x 100 = .33 x 100, or 33 percent. Thus, when there are seven poles in the system, the difference in strength between the two opposing coalitions is one third as great as in a tripolar system. This means that, assuming units of equal size, alliance formation for offensive purposes is extremely destabilizing in a tripolar system, much less destabilizing in a quintipolar system, and still less destabilizing for a system of seven or more actors. (I define stability as the preservation of all actors in the system). 10
Tripolar systems are also particularly prone to indirect effects—systemic outcomes that do not correspond to the intentions of the actors. 11 For instance, given a tripolar system composed of three equally sized units, an increase in either hostility or cooperation between any two poles will, ceteris paribus, heighten the motivation to gang up against one of the poles. Why increased hostility between two poles should result in instability requires no explanation. Some readers, however, are wondering how increased cooperation between two poles likewise causes instability. The connection is not an obvious one because the outcome (system instability) is typically an indirect effect.
To illustrate, suppose each pole earmarks half of its unreserved forces against each of the other two poles. Now, imagine that poles A and B reciprocally reserve or demobilize all or some substantial part of the forces that each has been deploying against the other. They now have more forces and/or resources to target against C. Consequently, C’s defense has been made less secure with respect to both A and B, whether or not the action was designed to have this effect. 12 Arthur Lee Burns states the axiom this way: “The closer the alliance between any two or more Powers, the greater the increase of opposition or ‘pressure’ (other things being equal) between any one of the two and any third Power or group of Powers.” 13
In general terms, this means that an equilateral tripolar system has a greater chance of maintaining stability when bilateral contacts between the poles are of low frequency and intensity. This conclusion is similar to that reached by Deutsch and Singer, who, noting that an increase in the number of poles leads to an increase in their opportunities to interact, posited that systems of five or more actors are more stable than lesser number systems. The logic is straightforward: the large number of dyadic pairs divides the actors’ attention, producing bilateral relations of low intensity and high flexibility. 14
The problem is that low–level contact among the poles—the hypothesized condition that produces stability in systems of more than two actors—is extremely unlikely in a tripolar system: the small number of actors enables and encourages each member of the triad to focus its energies on the activities of the others. Ironically, the same logic that underpins Waltz’s argument about the stability of bipolar systems—the higher attention, greater flexibility, and reduced uncertainty of two–actor systems compared with that of larger–numbered systems—leads to the opposite conclusion under tripolarity. The additional pole, while only slightly diminishing each actor’s ability to concentrate on the others, means that no pole can rely solely on its own internal means to balance the other two. To survive, each pole must ensure that a hostile coalition does not form against it, and so each strives for a coalition with one of the other two members. But any coalition throws the system wildly out of balance, gravely endangering the isolated third.
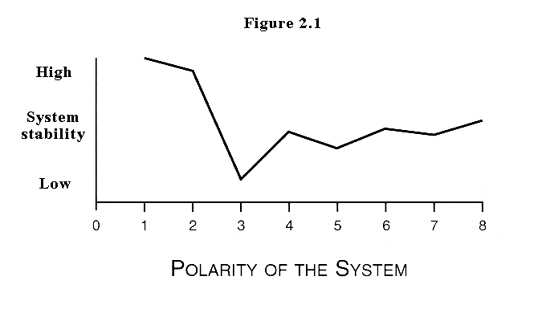
In sum, the perverse effects of tripolar dynamics turn the logic of bipolar stability on its head: increased attention, certainty, and flexibility yields extreme instability. The difference is that in a bipolar system each pole is certain that it can rely on its own resources to balance the other, while in a tripolar system each member is certain that it cannot balance the other two solely by internal means and, more important, that any alliance forms a winning coalition. For this reason, if we consider only systems composed of all power–maximizing actors (an assumption that will be relaxed when I discuss tripolar dynamics in greater depth), tripolar systems are the most unstable.
As shown in figure 2.1, one may conceptualize the relationship between polarity and stability as curvilinear, not monotonic, as is commonly assumed within the literature. Uni– and bipolar distributions are generally acknowledged to be the most stable systems because balancing is accomplished by internal rather than external means. By contrast, balancing in multipolar systems requires coalition formation. As a result, the stability of multipolar systems is low to moderately stable, depending on the number of poles: even–numbered systems are more stable than odd–numbered ones. Under multipolarity, however, stability increases as the number of poles grows because there will be more blocking coalitions, greater interaction opportunities, and greater alliance flexibility. In addition, as the number of poles increases, so too does the chance of maintaining a divisible peace, that is, local conflicts are less likely to explode into system–wide war.
Aside from their unique structural properties, tripolar systems should be studied because they have existed and will continue to exist in the real world. In fact, many current observers believe that, with the demise of the Soviet Union, the post–Cold–War system is rapidly becoming a tripolar one composed of the United States, Japan, and Germany. (I discuss the emerging tripolar world in the concluding chapter.)
Analysis of Five Types of Tripolar Systems
To analyze the properties of tripolarity, I have borrowed hypotheses from sociological theories of coalition formation in triads. 15 In particular, the present study has been influenced by the work of the sociologist Theodore Caplow. 16 Citing six basic power configurations of the triad, Caplow suggests that “under certain conditions the formation of particular coalitions depends upon the initial distribution of power in the triad and may be predicted to some extent when the initial distribution of power is known.” 17 Regarding the “certain conditions,” Caplow assumes that: (1) a stronger member always defeats a weaker member and will seek to do so, (2) strength is additive, (3) each member seeks to defeat the others, preferring the defeat of two others to the defeat of one (4) all states prefer more territory to what they currently possess. 18
Caplow’s analysis of alliance formation takes place in a Hobbesian, all–against–all world. The triad exists unwillingly: it comprises three hostile states, each seeking the destruction of the others. Members seek coalitions for both defensive and offensive motives, for protection and aggrandizement. The security objective of the alliance is to defeat a potential hegemon and/or to prevent the formation of a threatening two–against–one coalition. The offensive incentive for alignment is the added strength gained by the defeat and partition of the isolated third member.
Building on Caplow’s analysis, my theoretical framework adds the concept of state interest, that is, the mix of revisionist and status–quo states. As Simmel’s work suggests, the identities of the units play an important role in determining the stability of coalition behavior within a given triad. Unlike Caplow, therefore, I do not interpret anarchy to mean that all units are mutually hostile and/or power–maximizers; interests as well as the distribution of power affect coalition behavior in the triad. For the purpose of simplifying the analysis, however, state interest is treated as a dichotomous variable: states are either revisionist or status quo.
Configurations of Tripolar Systems
Given the definitional requirement that the weakest pole must have half the resources of the strongest pole, there are five possible tripolar power configurations:
Definitions
Assumptions
Among other things, this last assumption and the inclusion of status–quo states distinguishes the present analysis from that of Niou, Ordeshook, and Rose. 19 Glenn Snyder notes in his critique of Niou, et al. that their assumption of infinitely divisible and freely transferable resources 20 allows the authors to assert
| that states will voluntarily cede resources to a stronger challenger or attacker if necessary to avoid elimination and that, in turn, the challenger will accept the resource transfers in preference to gaining the same amount by war. . . Hence, the device of peaceful ceding of resources was introduced to permit the third party to save itself. . . by buying off a member of the threatening coalition at a price short of suicide. The logical fit between bargaining–set theory and a desired theoretical outcome—stability—was improved, but at considerable cost to empirical realism. 21 |
Thus, Niou et al. find, but I do not, that “the key feature of a three–country system is that no nation will be eliminated.” 22
Conversely, Wagner’s analysis of three–actor systems assumes, as I do, that “the power of states can only be increased by conquest.” 23 But in contrast to my assumption that the spoils are divided proportionately among the victors, Wagner assumes that states can only absorb the victim’s “resources at a maximum rate of r units per ‘day’ “ and “if two states are at war with a third, the rates at which they can each absorb the third’s resources are determined. . . by how the victim targets its resources at the two opposing states.” 24 Given the rules of Wagner’s game, it follows that the victim must target its resources unequally, thereby forcing the more–opposed attacker to defect before the less (or un–) opposed attacker gains more than half the resources of the system. Thus, Wagner concludes, while I do not, that no actor is ever eliminated in a three–actor system.
The usefulness of Wagner’s extra assumptions is an empirical question. The events of World War II, however, provide no examples of a two–against–one attack in which one of the attackers defected to join the victim’s side. There is evidence to the contrary, however: Germany and the Soviet Union eliminated Poland with neither attacker defecting against its partner; and, though Hitler tried to cope with Nazi Germany’s imminent defeat by offering alliances to the Soviet Union and the United States, neither defected to Germany’s side. I suspect that, in the real world, the importance of acquiring and keeping a reputation for alliance loyalty deters some states from double–crossing their partners by absorbing more than their fair share of the spoils or by defecting when the victim offers a better deal. Anarchy does not mean, as Wagner implies, that agreements between allies are unenforceable, but rather that they must be self–enforcing. 25 Because trust as well as power is an essential ingredient for present and future cooperation, allies rarely double–cross their partners, even though game–theoretic logic says otherwise.
Type 1. The Equilateral Tripolar System: A = B = C
This power configuration represents, ceteris paribus, the most unstable of all systems because a system of three equally powerful states cannot be balanced by alliance formation. While this is true of any odd–numbered system composed of equal units, the imbalance is proportionally greatest in this triad, where A and B combined possess 66 percent of the total resources, as against C’s 33 percent share. 26
Stabilizing an equilateral tripolar system, therefore, requires each pole to prevent the formation of a hostile alliance of the other two poles against itself. Although the power configuration heightens the tendency to gang up, the specific mix of revisionist and status–quo poles greatly affects system stability.
a. One revisionist pole
Given only one revisionist pole, a stable system should result. Potential aggression will likely take the form of the lone revisionist pole attacking the nearest status–quo pole. But such an attack is improbable because individual aggression in tripolarity tends to be self–defeating. On the one hand, if a stalemate results (and this is most likely among equally powerful poles) both combatants are weakened in relation to the neutral third, who obviously has no incentive to join the fray. On the other, if the revisionist pole appears to be winning, the neutral third must join the status–quo pole to ensure its own survival. Consequently, war is unlikely because the revisionist attacker can expect only a war of attrition or certain defeat.
A geographically distanced pole may assume one of four roles: 1) tertius gaudens, 2) the abettor, 3) the eyewitness, or 4) the mediator. The first two are likely to be played by a revisionist pole, the latter two by a status–quo pole. As tertius gaudens (the enjoying third) the remote pole turns the dissension of the two geographically proximate poles to its own advantage by asking an exploitative price for its support. As the abettor, it instigates conflict between the other members of the triad for its own purposes. In the role of eyewitness, it does nothing and seeks nothing from the conflict. In the mediator role, it declares neutrality toward the conflict and works to stabilize the triad. 27
b. Two revisionist poles
A tripolar system composed of two revisionist poles is typically unstable because both power–maximizers are highly motivated to augment their resources at the expense of the lone status–quo pole. As a result, the two revisionist poles can be expected to put aside their competition temporarily so as to make substantial gains. And because the winning coalition consists of two equally powerful partners, each member can expect to gain half the spoils, such that neither pole will be left vulnerable to the other after the war. Hence, there is little to prevent the partitioning of the isolated status–quo state. Eliminating a member of the triad transforms the system into a relatively stable but competitive bipolar system, as the two remaining poles (both power maximizers seeking gains at the other’s expense) are expected to resume their rivalry.
A favorable geographic position may temporarily protect the lone status–quo pole, but it will not appreciably stabilize this type of tripolar system. Suppose that the two revisionist poles are in close geographical proximity and the status–quo pole is distanced from them. The triad contains, in effect, two subsystems: one bipolar, the other unipolar, wherein the rivalry between the two revisionist poles protects the remote status–quo pole by preventing them from ganging up against it. The status–quo power may assume the role of either “the enjoying third” or the “abettor.” In either case, it remains on the sidelines, hoping that the two revisionist poles will bleed each other to death.
But this is a dangerous strategy for the status–quo power because one of the revisionist poles may be able to defeat the other by either forming a winning alliance with one or more revisionist powers or by devouring weaker states until enough additional resources are acquired to defeat the nearest pole. Once accomplished, the victorious revisionist pole would be in control of at least twice as many resources as the lone status–quo pole. (Hitler’s use of this strategy and why it failed will be discussed in chapters 4–6.)
c. Three revisionist poles
In this case, in which all three members are of equal strength and are revisionist powers, any possible coalition—AB, BC, and AC—is equally likely, making it an extremely volatile situation. All three members seek coalition, since isolation means extinction. But the structure of this type of tripolar system prohibits external “balancing” behavior (alliances for the purpose of counterbalancing a stronger or more threatening power or alliance) because any coalition easily defeats the isolated third member. ln addition, since all three members are revisionist powers, each pole must always be suspicious of the other two and none can enjoy true long–term security. Consequently, this system should exhibit the tendency to evolve into a stable bipolar system, as two poles will be tempted to destroy the isolated third to gain lasting security. Eliminating one pole through partitioning should not present major difficulties because each member of the winning coalition is of equal strength and is therefore entitled to an equal share of the spoils.
d. Three status–quo poles
This, of course, is the most stable tripolar system because all members share an interest in preserving the status quo. In this system, in which no pole seeks the elimination of any other, the continued integrity of the three actors is virtually assured. System stability simply requires the poles to make their intentions known, avoid provocative acts, and coordinate and consult with the others about their individual foreign policies. Their tacit agreement not to attack each other may be formalized by mutual nonaggression pacts between all dyads and/or a collective security arrangement, whereby each member pledges to come to the aid of the victim of an armed attack.
I should note that Glenn Snyder has portrayed the so–called “alliance dilemma” differently. Snyder assumes that, in a multipolar setting composed of equally strong actors, status–quo states will prefer the outcome of all–around abstention from alliances to a situation of two rival coalitions; but each state’s first choice is to form its own alliance while others abstain from doing so. According to this preference ordering, what Snyder calls “the primary alliance game” (the initial decision to align or abstain from alignment) follows the logic of an N–person prisoner’s dilemma (PD). 28 The problem with this argument, however, is that, in light of the significant costs of alliances in terms of treasure and political autonomy, why should states prefer a situation in which they alone form an alliance to one in which no alliances form in the first place? Given Snyder’s first assumption that “no state is aggressive, but none can know the intentions of others,” 29 the aligned state simply winds up paying the costs of alignment while gaining no real security benefits, just peace of mind.
Rather, when all actors are satisfied with the status quo, the primary alliance game is not a PD but a coordination problem known as “stag hunt” that is easily resolved by communication. No actor has any incentive to misrepresent or withhold private information regarding its true intentions, military capabilities and doctrine, or resolve to uphold the status quo. To the contrary, every member has an incentive to announce its benign intentions, to make costly signals to confirm them, and to avoid miscalculation. It is illogical to think that a small number of rational actors would have trouble reaching the efficient solution of no alliances, if coordination were in fact the only problem here. 30
Realists would no doubt counter that the condition of international anarchy (understood as the absence of a sovereign arbiter to make and enforce agreements among states) creates uncertainty, such that states can never know or entirely trust each others’ stated intentions. 31 Indeed, even if all states are confident that none secretly harbors aggressive aims, intentions can change. Uncertainty about the future impels prudent states wishing to survive to fear the worst and assume the costs entailed therein. Realists would also invoke the related argument of the security dilemma, the fact that a state’s efforts to make itself more secure often have the unintended but inescapable effect of making others less secure. The pernicious effects of anarchy and the security dilemma, they argue, mean that rival alliances may form even when all states prefer that no coalitions emerge.
The problem with these arguments is that they ignore the availability or feasibility of bargains that would avoid the costs of alliances. If no state seeks to revise the status quo by force of arms, there is no reason why signaling and bargaining cannot prevent the inefficient outcome of alliance formation—an outcome that would only create unwanted hostility within the triad and that could trigger the far higher costs and dangers of a war down the road. When offensive military postures are distinguishable from defense ones, there is no security dilemma, as Jervis himself acknowledges. 32 Moreover, costly signals are easiest to make (that is, most effective in communicating the state’s intentions) when technology and geography favor offensive military strategies and force structures. As I have written elsewhere:
Under such conditions, security–seeking states can easily signal their benign intentions by spending heavily on defense to compensate for the advantage of offense. Other states should have no trouble inferring the true intentions of a state willing to engage in this kind of costly signaling. It is thus precisely when offense has the advantage that security–seeking states must cooperate to achieve security, and can easily do so. 33
When offense has the advantage but it is not distinct from defense, the security dilemma is most intense. In such a world, however, the high risks of war (especially unwanted, inadvertent war) provide status–quo states with great incentives to seek security through cooperative means. Even under these conditions, which are least favorable for security regime formation, it is not at all obvious that states will choose individualistic policies and alliances over reliance on joint measures. 34 For these reasons, when all members of a triad support the status quo, no alliances will form. This “no alliance” prediction holds not only for equilateral tripolar systems but also for any power configuration consisting of all status–quo actors.
Type 2. The Paradox of Power: A > B = C, A < B + C
a. Three revisionist poles
In this type of tripolar system, A is slightly stronger than B and C, which are equally sized; but A is weaker than the combined strength of B and C. All three members strive for a coalition, as any combination defeats the isolated member. Paradoxically, under such circumstances, A’s strength proves to be a handicap, since both B and C find A less attractive as a coalition partner than each other. This is true because, in either an AB or AC alliance, A would be in control of its weaker partner. Consequently, A, in a coalition with either B or C, would be expected to gain at least an equal share of the rewards, and probably the lion’s share—further disadvantaging the weaker ally, who must receive the bulk of the reward to gain security. Alternatively, a BC coalition (in which both B and C are of equal strength) secures an equal distribution of the reward and does not threaten either member.
This is the logic behind William Gamson’s theory of the “cheapest winning coalition.” Under the assumption that “any participant will expect others to demand from a coalition a share of the payoff proportional to the amount of resources which they contribute to a coalition,” 35 Gamson deduces the logic of the cheapest winning coalition:
When a player must choose among alternative coalition strategies where the total payoff to a winning coalition is constant, he will maximize his payoff by maximizing his share. The theory states that he will do this by maximizing the ratio of his resources of the total resources of the coalition. Since his resources will be the same regardless of which coalition he joins, the lower the total resource the greater will be his share. Thus, where the total payoff is held constant, he will favor the cheapest winning coalition. 36
Gamson’s theory of the cheapest winning coalition predicts a BC pairing for this triad, as it maximizes B and C’s share of the benefits for the same amount of resources.
b. One or two status–quo poles
When there is a mix of status–quo and revisionist states, the alliance patterns within this system become considerably more complex. If A is a status–quo pole, for instance, either B or C may align with it against the isolated third. Such an alignment is especially likely if either B or C is also a status–quo state, in which case an overpowering status–quo coalition will form to oppose the lone revisionist member of the triad.
If B and C are mutually hostile, A is in the enviable position of holding the balance, and so it can play the role of either balancer or kingmaker. As balancer, it seeks to preserve a stalemate between the two rivals. As kingmaker, it sells its services to the highest bidder. The motto of the kingmaker is: “Cui adhaereo prae est,” translated as “the one that I join is the one which will turn the scales” or “the party to which I adhere getteth the upper hand.” 37 When A is a status–quo state, it will likely adopt the role of balancer working for system stability; as a revisionist state, A is most likely to be an opportunistic kingmaker.
Britain prior to the twentieth century, when it was still the most powerful European state and a defender of the status quo on the continent, is the prototypical example of the balancer. Pointing out that Britain might well have played the role of kingmaker, Churchill proudly proclaims:
| Faced by Philip II of Spain, against Louis XIV under William II and Marlborough, against Napoleon, against William II of Germany, it would have been easy and must have been very tempting to join with the stronger and share the fruits of his conquest. However, we always took the harder course, joined with the less strong Powers, made a combination among them, and thus defeated and frustrated the Continental military tyrant, whoever he was, whatever nation he led. 38 |
Table 2.1 Percentage Distribution of the COW
Index Among the Major Powers and the Polarity of the International System, 1890-1980.
| Year | #poles | US | Jap | Ger | UK | Rus | Fr | It | A–H | |
|---|---|---|---|---|---|---|---|---|---|---|
| 1890 | 5 | 19.6* | 3.4 | 15.9* | 21.0* | 15.0* | 12.7* | 5.3 | 7.1 | |
| 1900 | 4 | 21.6* | 3.8 | 16.7* | 20.6* | 16.1* | 10.1 | 4.9 | 6.1 | |
| 1913 | 4 | 25.0* | 4.4 | 18.2* | 14.1* | 16.7* | 10.4 | 5.0 | 6.1 | |
| 1925 | 1 | 34.9* | 7.8 | 11.6 | 15.4 | 13.1 | 10.8 | 6.3 | – | |
| 1934 | 2 | 28.8* | 8.9 | 13.9 | 9.5 | 23.2* | 9.3 | 6.2 | – | |
| 1938 | 3 | 22.5* | 9.3 | 20.1* | 10.5 | 24.9* | 6.9 | 5.3 | – | |
| 1950 | 2 | 38.0* | 7.0 | 8.1 | 9.8 | 31.4* | 5.7 | – | – | |
| 1960 | 2 | 37.0* | 8.7 | 7.5 | 7.9 | 32.3* | 6.6 | – | – | |
| 1970 | 2 | 34.7* | 12.0 | 7.2 | 6.4 | 34.7* | 5.0 | – | – | |
| 1980 | 2 | 30.3* | 13.0 | 7.7 | 5.5 | 38.1* | 5.4 | – | – |
* ¡ Polar Power source: “Correlates of War Capability Data Set Printout,” Inter–University Consortium for Political and Social Research at the University of Michigan, July 1990.
Churchill correctly points out that Britain, had it been a greedy revisionist state, would have bandwagoned with the aggressor to share in the spoils of victory. Other opportunistic strategies would also have been available. As a kingmaker, Britain could have bribed the weaker side for its assistance. If it were particularly devious, Britain might have instigated conflict on the Continent and then worked for a stalemate in order to gain relative to all the beleaguered combatants.
d. Three status–quo poles
When all three poles are status–quo states, no coalition is predicted. For reasons outlined above, this “no coalition” prediction holds for any system composed of all status–quo units.
Type 3. The Partitioned Third: A < B = C
When both B and C are revisionist, A cannot align with either because once the coalition has partitioned the isolated member of the triad, A will be destroyed by its stronger ally. The only remaining alliance, therefore, is BC, which can safely partition A because its members are of equal strength. For security reasons, B and C should seek to partition A: B must block AC and C must prevent AB. Therefore, the most likely scenario is the formation of a BC coalition for the purpose of partitioning A and achieving an equal balance between B and C.
However, if B and C are mutually hostile, is not it clearly in A’s interest to prolong their rivalry by acting as a balancer, gaining at the expense of the other two poles? In the short run, yes; but in the long run, no. This is because the role of balancer is a dangerous one for the weakest member of the triad. The balancer must guarantee through skillful diplomacy that the two warring poles do not temporarily set aside their differences to gang up against it. This is no easy task for A. By playing the role of balancer and continually frustrating the desires of B and C, A will engender hostility with both B and C. Given the animosity directed against the balancer, one would expect this role to be played by a state that was considerably stronger than the other two, not by the weakest triadic member.
Type 4. The Balanced Tripolar System: A = B + C, B = C
Although somewhat counterintuitive, a stable tripolar system is most likely to obtain (other things being equal) when at least some of the poles are of unequal weights. Consider, for instance, a system of three revisionists states, where A = B + C. Because A is “near–preponderant” (it possesses half of the power resources in the system) and it seeks to increase its power, B and C realize that to survive they must align to counterbalance A. This type of tripolar system is essentially a behavioral dyad, and so it exhibits the high stability associated with bipolarity. 39
Conversely, when the near–preponderant member of the triad is a status–quo power, an alliance between B and C is not required for their survival. Indeed, if either B or C is a status–quo power, it may align with A against the isolated revisionist pole. Moreover, given my definition of a pole, B and C must be of equal strength whenever their combined resources equal those of A (since no pole can have less than half the resources of the most powerful pole). As a result, a hostile bipolar stalemate may exist between B and C, leaving A to play the role of mediator, abettor, eyewitness, or tertius gaudens (see discussion above.)
Type 5. The Unbalanced Tripolar System: A > B > C, A < B + C
Less obvious is the inherent stability of a tripolar system where all of the poles are of different strengths: A > B > C, and A < B + C. To illustrate the peculiar dynamics of this system, consider a tripolar system in which the power ratio among the three poles is A = 4, B = 3, C = 2. Let us further assume that all members of the system are revisionist powers. At first glance, this system appears to be extremely unstable (i.e., one of the actors will be eliminated) and warprone, since any contest between two actors is decisive and any coalition is a winning coalition. Yet, this type of triad proves to be one of the simplest and most stable forms of a balance of power.
First, consider an isolated attack within this triad. In such a situation, it is immediately obvious to the third power that it must block the efforts of the attacker by joining the weaker side, or else be dominated by the victor. The attacker not only knows that the third power must resist its efforts to destroy the initial victim, but also that it has no hope of prevailing against such a coalition. Hence, a stronger member of the triad will not be tempted to try to defeat a weaker member by means of an isolated attack; the dynamics of the system discourage offensive actions.
Now let us consider an attack by a coalition against an isolated third pole. Although every coalition is a winning coalition, all pairings in a 4–3–2 triad are unbalanced—they consist of a stronger and a weaker member. Thus, if any coalition formed, went to war, and won as expected, the system would be transformed into a dyad with the weaker member of the winning alliance at the mercy of its stronger partner. The weaker ally will be imperiled even if the spoils of victory are divided equally, rather than according to each member’s proportionate resources. 40
In summary, given the dynamics of this system, any pairing will inevitably result in only one remaining actor; because this is obvious to all three poles, no coalition will form in the first place. Hence, although all actors are power maximizers and every pairing forms a winning coalition, the perverse effects of the unbalanced triad virtually assure the continued integrity of all the actors and the absence of war among them. This is true for all mixes of revisionist and status–quo states except for the following case.
Two status–quo poles
Ironically, when there are two status–quo poles, the system is potentially unstable. In this situation, the status–quo poles may be motivated, for defensive purposes, to wage a preventive war to eliminate the revisionist pole, which poses a latent (if not immediate) threat to their individual security.
The Enhanced Role of LGPs and Other Nonpoles Under Tripolarity
To this point, the discussion has been limited to the behavior of only polar powers. While this analysis leads to broad expectations about the overall stability of the five types of tripolar systems, it will not take us very far in explaining the specific dynamics of a given historical case. For this we need to consider the behavior of lesser great powers as well as poles. Indeed, the behavior of LGPs plays an important role in determining the stability of tripolar systems—a subject to which we now turn.
Empirically, LGPs have had the greatest effect on the stability of tripolar and, to a lesser extent, quadrapolar systems. By contrast they have had only a moderate effect on the stability of unipolar systems, and hardly any effect on the stability of multipolar (5 or more poles) and bipolar systems. A look at the distribution of capabilities within the Major–Power subset for the past 100 years shows why this proposition has held and will continue to do so. (See Table 2.1, below.)
Under bipolarity, the system’s capabilities tend to be highly concentrated in the two poles with only a small proportion left over to be divided among the many remaining states. The huge capability disparity between the two polar powers and the remaining states makes it highly unlikely that a significant amount of LGPs—whose total power could affect the stability of the system—will exist in a bipolar system. Bipolarity results instead in a two–level distribution of capabilities: polar powers and insignificant lesser states (sometimes referred to as inessential actors) of varying sizes.
Conversely, under multipolarity (five or more poles), the system’s capabilities are widely dispersed among the many poles, such that most of the significant actors are of roughly equal strength (i.e., 1890). Because the number of Great Powers (that is, poles and LGPs) in the international system has never exceeded eight, only one or two, if any, LGPs will exist under multipolarity, and they will be too weak and few in number to affect the polar balance. There are two reasons for this.
First, increasing the number of poles in the system produces a leveling effect that results in rough equality among the major powers. As multipolarity is not characterized by wide disparities among the major actors, we should not expect to find many LGPs, since most of the system’s capabilities reside in the many poles. Second, as the number of poles increases, the impact of each pole on the stability of the system decreases, resulting in a corresponding decrease in the importance of each individual LGP. Consequently, a large number of LGPs will be required to affect the polar balance of power in a multipolar system, and this is mathematically improbable, if not impossible.
By contrast, the distribution of capabilities in tripolar systems—and to a lesser degree in four–pole systems—is not as highly concentrated as in bipolarity or as diffuse as in multipolar systems of five or more actors. In tripolar systems, the poles do not dwarf the other states in the system as they do in bipolarity, and so the balance is more easily tipped by strong LGPs than in multipolar systems of five or more actors. As a result, we should expect to find influential nonpolar actors in tripolar (e.g., 1938) and quadrapolar systems (e.g., 1900–1913).
Lastly, by definition, a unipolar system means that every Great Power with the exception of the hegemon must be a nonpolar power. Sheer numbers alone suggest that LGPs will play a significant role in the stability of unipolar systems. Numbers alone, however, are somewhat misleading. Given its exalted power position, the hegemon should be both willing and able to maintain the stability of the system, which, after all, has obviously been working to its own advantage. Yet, as the United States proved in the 1920s, hegemons have not always been willing to assume the role of system manager. The U.S.’s refusal to assume hegemonic leadership during the unipolar period of the 1920s, however, was largely a consequence of its being an artificial hegemon (that is, unipolarity was, in this case, a temporary effect of the Great War, as was the bipolar system of 1934). But, even here, the absence of hegemonic leadership did not enhance the importance of nonpoles on the stability of the system. Instead, the system remained relatively peaceful until the mid–1930s, when Germany and the Soviet Union returned to polar strength. In other words, it was not the free reign of nonpolar powers under unipolarity that caused the instability leading up to the Second World War; rather system instability occurred when two additional poles emerged to create a tripolar system.
In sum, the high capability concentration in bipolarity and the low capability concentration in multipolarity suggest that it is unlikely that LGPs will appear in either system and/or, if they do exist, that they will have a significant effect on the stability of the system. Conversely, the moderate concentration of power in tripolar and quadrapolar systems (and to a far lesser extent, unipolar systems) is conducive to the existence of LGPs in sufficient numbers and strength to affect the power situation among the poles. The impact of LGPs on system stability and alliance patterns will be greatest, however, under tripolarity. The next chapter brings these nonpolar states back into the analysis; and unlike the preceding analysis of tripolar systems, the theoretical discussion and hypotheses in chapter 3 apply to all classes of balance–of–power systems, that is, bipolar, tripolar, and multipolar.
Endnotes
Note 1: Of course, polarity is not the only way to define the structure of the international system. For studies that define international structure in terms of its concentration of capabilities rather than its polarity, see J. David Singer, Stuart Bremer, and John Stuckey, “Capability Distribution, Uncertainty, and Major Power Wars, 1820–1965,” in Bruce M. Russett, ed., Peace, War, and Numbers (Beverly Hills, Calif.: Sage Publications, 1972), pp. 19–48; James Lee Ray and J. David Singer, “Measuring the Concentration of Power in the International System,” Sociological Methods and Research, vol. 1, no. 3 (May 1973), pp. 403–437; Edward D. Mansfield, “The Concentration of Capabilities and the Onset of War,” Journal of Conflict Resolution, vol. 36, no. 1 (March 1992), pp. 3–24. For a rule–oriented definition of the international system, see Paul W. Schroeder, The Transformation of European Politics, 1763–1848 (New York: Oxford University Press, 1994), p. x. Back.
Note 2: For an insightful discussion of polarity, see David P. Rapkin, “Concept (Mis)formation in International Systems Research: Polarity and Polarization,” draft manuscript, University of Nebraska–Lincoln, February 16, 1993. Back.
Note 3: Gilpin, War and Change, p. 235. Back.
Note 4: Morton A. Kaplan, System and Process in International Relations (New York: Wiley, 1957), p. 34. Back.
Note 5: Waltz, Theory of International Politics, p. 163. Back.
Note 6: Ostrom and Aldrich, The Relationship Between Size and Stability, p. 766. Back.
Note 7: David Garnham, “The Causes of War: Systemic Findings,” in Alan Ned Sabrosky, ed., Polarity and War: The Changing Structure of International Conflict (Boulder, Colo.: Westview Press, 1985), p. 20. Back.
Note 8: George Simmel, “The Number of Members as Determining the Sociological Form of the Group,” American Journal of Sociology, vol. 8, no. 1 (July 1902), pp. 45–46. Back.
Note 9: Claude, Power and International Relations p. 13. Back.
Note 10: Note that this definition of system stability, which I have borrowed from R. H. Wagner, does not mean peace. Wagner writes: “I will say that an international system is stable if the independence of all the actors in it is preserved. Thus, if a theory leads to the prediction that one or more of the states in a system will be eliminated, I will say that that system is, according to the theory, unstable. Peace will be defined as the absence of war. Thus, an international system can be stable even though it is characterized by frequent wars in which many states are deprived of significant portions of their territory, so long as no state is completely eliminated.” Wagner, “The Theory of Games and the Balance of Power,” pp. 546–547. Niou, Ordeshook, and Rose use the same definition, and they also distinguish system stability from resource stability. See Niou, Ordeshook, and Rose, The Balance of Power . For an interesting critique of this work, see Snyder, “Alliances, Balance, and Stability,” pp. 132–142. Back.
Note 11: For a description of indirect effects, see Robert Jervis, “Systems and Interaction Effects,” pp. 26–29. Back.
Note 12: This analysis is drawn from Arthur Lee Burns, “From Balance to Deterrence: A Theoretical Analysis,” World Politics , vol. 9, no. 4 (July 1957), pp. 494–99. Back.
Note 14: For the “interaction opportunity” hypothesis, see Deutsch and Singer, “Multipolar Power Systems and International Stability.” Back.
Note 15: The two literatures of balance of power theory and sociological theories of coalition formation seem immediately relevant to each other. As Dina Zinnes remarks, “The sociological literature contains theories which specifically predict the membership of winning coalitions as a function of the distribution of power within the group. Thus it would seem that the international relations specialist could gain insight into the balance of power theory by studying the sociological literature.” Dina A. Zinnes, “Coalition Theories and the Balance of Power,” in Sven Groennings, E. W. Kelly, and Michael Leiserson, eds., The Study of Coalition Behavior: Theoretical Perspectives and Cases From Four Continents (New York: Holt, Rinehart & Winston, 1970), pp. 351–352. Back.
Note 16: Theodore Caplow, Two Against One : Coalitions in Triads (New Jersey: Prentice Hall, 1968); Caplow, “A Theory of Coalitions in the Triad,” American Sociological Review, vol. 21, no. 2 (August 1956), pp. 489–493; Caplow, “Further Development of a Theory of Coalitions in the Triad,” American Journal of Sociology, vol. 64, no. 5, (March 1959), pp. 488–493. Other important works include: Theodore Mills, “Power Relations in Three–Person Groups,” American Sociological Review, vol. 18, no. 4, (August 1953), pp. 351–357; Mills, “The Coalition Pattern in Three–Person Groups,” American Sociological Review, vol. 19, no. 6 (December 1954), pp. 657–667; William A. Gamson, “A Theory of Coalition Formation,” American Sociological Review, vol. 26, no. 3 (June 1961), p. 376; Simmel, “The Number of Members as Determining the Sociological Form of the Group,” pp. 1–46, 158–196; Simmel, “The Triad,” in Kurt H. Wolff, (trans., ed., intro.) The Sociology of George Simmel (New York: Glencoe Press, 1950), pp. 145–169; Sheldon Stryker and George Psathas, “Research on Coalitions in the Triad: Findings, Problems and Strategy,” Sociometry, vol. 23, no. 3 (September 1960), pp. 217–230; Harold Kelly and A.J. Arrowood, “Coalitions in the Triad: Critique and Experiment,” Sociometry, vol. 23, no. 3 (September 1960), pp. 231–244; A. Paul Hare, Edgar F. Borgatta, and Robert F. Bales, eds., Small Groups: Studies in Social Interaction (New York: Alfred A. Knopf, 1966). Back.
Note 17: Caplow, Two Against One , p. 22; Caplow, “A Theory of Coalitions in the Triad,” pp. 489–93; Mills, “Power Relations in Three–Person Groups”; Mills, “The Coalition Pattern in Three–Person Groups.” Back.
Note 18: Caplow, Two Against One , pp. 21–6; idem, “A Theory of Coalitions in the Triad,” pp. 489–493; idem, “Further Development of a Theory of Coalitions in the Triad,” pp. 488–493. Back.
Note 19: Niou, Ordeshook, and Rose, The Balance of Power , pp. 93–97. Back.
Note 21: Snyder, “Alliances, Balance, and Stability,” pp. 134, 136. Back.
Note 22: Niou, Ordeshook, and Rose, The Balance of Power , p. 95. Back.
Note 23: Wagner, “The Theory of Games,” pp. 549, 554–559. Back.
Note 24: Ibid., 549–550. Back.
Note 25: See R. Harrison Wagner, “Peace and the Balance of Power in a Three–State World,” paper delivered at the Annual Meetings of the American Political Science Association. The New York Hilton, September 1–4, 1994. In this later work, Wagner makes the case for cheating by switching to the side of the victim but backs off, claiming that “incorporating such endgame moves explicitly in a model is difficult.” (p. 8) Given the new rules of Wagner’s game, his three–actor systems are now quite unstable. Back.
Note 26: For similar views of tripolar instability, see Caplow, Two Against One ; Lowell Dittmer, “The Strategic Triangle: An Elementary Game–Theoretical Analysis,” World Politics , vol. 33, no. 4 (July 1981), pp. 485–515; Brian Healy and Arthur Stein, “The Balance of Power in International History: Theory and Reality,” Journal of Conflict Resolution, vol. 17, no. 1 (March 1973), pp. 33–61; Waltz, Theory of International Politics, p. 163; Kaplan, System and Process, p. 34; and Morton A. Kaplan, Arthur Lee Burns, and Richard E. Quandt, “Theoretical Analysis of the ‘Balance of Power,’ “ Behavioral Science, vol. 5, no. 3 (July 1960), p. 244. For theorists who find three–actor games the most stable of all systems, see Garnham, “The Causes of War,” p. 20; Ostrom and Aldrich, “The Relationship Between Size and Stability,” p. 766; Niou, Ordeshook, and Rose, The Balance of Power , p. 95; and Wagner, “The Theory of Games,” p. 575. Back.
Note 27: I have borrowed the terms “abettor” and “eyewitness” from Liska, Nations In Alliance, pp. 163–164; “tertius gaudens” and “the mediator” are taken from Caplow, Two Against One , p. 20; Caplow borrowed them from Simmel, The Sociology of George Simmel , pp. 148–149. Back.
Note 28: Glenn H. Snyder, “The Security Dilemma in Alliance Politics,” World Politics , vol. 36, no. 4 (July 1984), pp. 461–496, esp. pp. 462–463. Back.
Note 29: Ibid., p. 462n. Back.
Note 30: This logic is drawn from James D. Fearon, “Rationalist Explanations for War,” International Organization , vol. 49, no. 3 (Summer 1995), pp. 379–414. My argument simply extends Fearon’s insightful analysis to alliances, which he does not cover. Back.
Note 31: See, for example, Michael Spirtas, “A House Divided: Tragedy and Evil in Realist Theory,” Security Studies , vol. 5, no. 3 (Spring 1996), pp. 409–412. Back.
Note 32: Jervis, “Cooperation Under the Security Dilemma,” p. 211. Back.
Note 33: See Schweller, “Neorealism’s Status–Quo Bias,” pp. 103–104. Back.
Note 34: For a slightly different view, see Robert Jervis, “Security Regimes,” in Stephen D. Krasner, ed., International Regimes (Ithaca, N.Y.: Cornell University Press, 1983), p. 178. Back.
Note 35: Gamson, “A Theory of Coalition Formation,” p. 376. Back.
Note 37: See Herbert Butterfield, “The Balance of Power ,” p. 138 and Martin Wight, “The Balance of Power ,” p. 159 in Butterfield and Wight, eds., Diplomatic Investigations: Essays in the Theory of International Politics (Cambridge: Harvard University Press, 1966). Back.
Note 38: Winston S. Churchill, The Gathering Storm (New York: Bantam, 1961), pp. 186–187. Back.
Note 39: Of this type of system, R. H. Wagner writes: “I conclude, then, that not only is any distribution stable which gives one player half the resources and divides the remainder unequally between the other two; but also, so long as no actor has more than half the resources in the system, any other type of distribution will be transformed into one of the former type in a three–actor game conducted according to the rules stated above. This type of distribution can be said to represent both inequality of power (among the individual states) and equality of power (between the two sets of opposing forces); it is also the only distribution in which one state has no choice but to come to the aid of another in order to prevent an aggressor from achieving supremacy.” Wagner, “Theory of Games and the Balance of Power,” pp. 558–559. I disagree with this assessment, however. As I discuss below, a system in which the resources of the three actors is in a 4:3:2 ratio is equally stable, though no actor possesses half of the total resources in the system. Back.
Note 40: Even supposing that the stronger member promises in advance to turn over the lion’s share of the spoils to its weaker partner, the latter still must reject the offer. This is because once the targeted pole has been eliminated, the stronger pole will no longer have any incentive—and it cannot be coerced—to comply with the agreement. Back.